Machine Learning¶

约 3021 个字 597 行代码 8 张图片预计阅读时间 23 分钟

参考

https://www.bilibili.com/video/BV1PN4y1V7d9/

抛去无意义的话，直接进入正题。

引入¶

假设我需要向银行借钱，银行根据我的年龄($x_1$),工资($x_2$),来决定贷款的额度(h)。

这相当于在一个空间直角坐标系中，拟合出一个最合适的平面。

记拟合的平面为$h_{\theta}(x) = \theta_0 +\theta_1 x_2+\theta_2 x_2$

记$\mathbf{x} = \begin{bmatrix} 1 \\ x_1 \\ x_2 \end{bmatrix}$,$\mathbf{\theta} = \begin{bmatrix} \theta_0 \\ \theta_1 \\ \theta_2 \end{bmatrix}$,则$h_{\theta}(x)=\theta^T x$

此外，我们还需要定义一个误差项$\epsilon$,因此现在对于每一个我们已知的样本点，如果用y来表示实际值，$y^{(i)}=\theta^T x^{(i)} + \epsilon^{(i)}$

对于误差$\epsilon^{(i)}$, 有如下性质：

独立：张三和李四都来贷款，他们俩能借到多少钱相互之间无关 -- 数据之间独立
同分布：他俩都得去同一家银行 -- 数据服从相同的概率分布，即每个误差项$\epsilon^{(i)}$都来自相同的分布。
标准正态分布：误差服从均值为0且方差为$\sigma^2$的正态分布，可以表示为： $ x \sim \mathcal{N}(0, \theta^2) $

似然函数¶

对于上面的案例，由于误差服从正态分布，其密度函数为$f(\epsilon^{(i)})=\frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(- \frac{(\epsilon^{(i)})^2}{2 \sigma^2}\right)$

我们用$y, x$来表示$\epsilon$，于是得到$f(y^{(i)}|x^{(i)}, \theta)= \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(- \frac{(y^{(i)} - \theta^T x^{(i)})^2}{2 \sigma^2}\right)$

似然函数定义¶

似然函数表示为所有观测值的联合概率密度函数

\[L(\theta) = \prod_{i=1}^{n} f(y^{(i)}|x^{(i)}, \theta) = \prod_{i=1}^{n} \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(- \frac{(y^{(i)} - \theta^T x^{(i)})^2}{2 \sigma^2}\right)\]

对数似然函数¶

有时为了简化计算，我们会取一个对数。

\[\ell(\theta) = \log L(\theta) = \sum_{i=1}^{n} \log \left( \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(- \frac{(y^{(i)} - \theta^T x^{(i)})^2}{2 \sigma^2}\right) \right)\]

进一步简化对数似然函数：

\[\ell(\theta) = n \log{\frac{1}{\sqrt{2 \pi} \sigma}} - \frac{1}{2\sigma ^2} \sum_{i=1}^n((y^{(i)} - \theta^T x^{(i)})^2)\]

现在再回过头来思考一下，我们的目的是什么呢？就是让似然函数越大越好。考虑上式中的变量，我们只需要让$\frac{1}{2}\sum_{i=1}^n((y^{(i)} - \theta^T x^{(i)})^2)$越小越好.

不妨记$J(\theta) = \frac{1}{2}\sum_{i=1}^n((y^{(i)} - \theta^T x^{(i)})^2)$

\[J(\theta) = \frac{1}{2} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2 = \frac{1}{2} (X\theta - y)^T (X\theta - y)\]

对$\theta$ 求偏导：

\[\nabla_\theta J(\theta) = \nabla_\theta \left( \frac{1}{2} (X\theta - y)^T (X\theta - y) \right) \]

\[= \nabla_\theta \left( \frac{1}{2} (\theta^T X^T X \theta - \theta^T X^T y - y^T X \theta + y^T y) \right)\]

\[= \frac{1}{2} \nabla_\theta \left( \theta^T X^T X \theta - \theta^T X^T y - y^T X \theta + y^T y \right)\]

\[= X^T X \theta - X^T y\]

要求极值点，因此偏导为0

\[\therefore \theta = (X^T X)^{-1} X^T y\]

梯度下降¶

上面的似然函数推导听上去很美好，X，Y都是已知的，我们只需要代进去就能得出$\theta$，然而,$X^T X$并不总是可逆的，这就意味着我们不能直接得出$\theta$的值。因此，需要引入梯度下降的概念。

概念¶

机器学习的主要目的是通过迭代地调整模型参数，以最小化损失函数。因为有许多目标函数是不可解的，因此，需要梯度下降的思想。

做法¶

梯度在数学的学习中都已经接触过，是一个多元函数在某点处变化最快的方向和速率，是一个向量，也是我们常说的方向导数。

假设现在我们的目标函数是$J(\theta)= \frac{1}{2m} \sum^m_{i=1}(y^i - h_{\theta}(x^i))^2$，初始先随机取$\theta$的值，为了不断更新$\theta$来让预测值和真实值更接近，有如下方法

批量梯度下降 (Batch Gradient Descent)¶

批量梯度下降使用整个训练集来计算梯度更新。

公式：

\[\frac{\partial J(\theta)}{\partial \theta_j} = -\frac{1}{m} \sum_{i=1}^{m} (y^i - h_{\theta}(x^i) )x^i_j\]

\[\theta^{\prime}_j= \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_{\theta}(x^i) - y^i)x^i_j\]

解释：

$\theta$：参数向量
$\alpha$：学习率
$m$：训练样本的数量
$h_{\theta}(x^i)$：模型的预测值
$y^i$：某个真实值
$x^i$：某个输入特征向量
$x^i_j$:某个输入向量与参数$\theta_j$相匹配的

随机梯度下降 (Stochastic Gradient Descent)¶

随机梯度下降每次只使用一个训练样本来更新参数。

公式：

\[\theta^{\prime}_j= \theta_j - \alpha (h_{\theta}(x^i) - y^i)x^i_j\]

解释：

$\theta$：参数向量
$\alpha$：学习率
$h_{\theta}(x^i)$：模型的预测值
$y^i$：某个真实值
$x^i$：某个输入特征向量
$x^i_j$:某个输入向量与参数$\theta_j$相匹配的

小批量梯度下降 (Mini-batch Gradient Descent)¶

小批量梯度下降使用一小部分训练样本（称为小批量）来计算梯度更新。

公式：

\[\theta^{\prime}_j= \theta_j - \alpha \frac{1}{b} \sum_{i=1}^{b} (h_{\theta}(x^i) - y^i)x^i_j\]

解释：

$\theta$：参数向量
$\alpha$：学习率
$b$：小批量的样本数量
$h_{\theta}(x^i)$：模型的预测值
$y^i$：某个真实值
$x^i$：某个输入特征向量
$x^i_j$:某个输入向量与参数$\theta_j$相匹配的

需要说明一下的是，学习率相当于是每次参数更新的步长大小，因为我们算出来的梯度只是在某一点的方向导数，并不能代表全部，所以更新的学习率需要仔细考虑。

线性回归模型实战¶

Normalize¶

Normalize就是将数据进行像正态分布一样的处理。

标准化的数学公式如下：

\[ z = \frac{x - \mu}{\sigma} \]

其中：

$x$ 为原始数据，
$\mu$ 为数据的均值，
$\sigma$ 为数据的标准差。

标准化通过减去均值并除以标准差，将数据转换为均值为0，标准差为1的正态分布。

Normalize

import numpy as np


def normalize(features):

    features_normalized = np.copy(features).astype(float)

    # 计算均值
    features_mean = np.mean(features, 0)

    # 计算标准差
    features_deviation = np.std(features, 0)

    # 标准化操作
    if features.shape[0] > 1:
        features_normalized -= features_mean

    # 防止除以0
    features_deviation[features_deviation == 0] = 1
    features_normalized /= features_deviation

    return features_normalized, features_mean, features_deviation

Sinusoids¶

生成正弦波特征

sinusoids

import numpy as np


def generate_sinusoids(dataset, sinusoid_degree):
    """
    生成正弦波特征。
    """
    # 获取数据集中的样本数量
    num_examples = dataset.shape[0]
    # 初始化一个空数组，用于存储生成的正弦特征
    sinusoids = np.empty((num_examples, 0))

    # 生成指定次数的正弦特征
    for degree in range(1, sinusoid_degree + 1):
        # 计算正弦值
        sinusoid_features = np.sin(degree * dataset)
        # 将新生成的正弦特征连接到 sinusoids 数组的列方向上
        sinusoids = np.concatenate((sinusoids, sinusoid_features), axis=1)

    # 返回生成的正弦特征数组
    return sinusoids

Polynomial¶

处理多项式特征。

Polynomials

"""Add polynomial features to the features set"""

import numpy as np
from .normalize import normalize


def generate_polynomials(dataset, polynomial_degree, normalize_data=False):
    """变换方法：
    x1, x2, x1^2, x2^2, x1*x2, x1*x2^2, etc.
    """

    # 将数据集按列分割成两个子集
    features_split = np.array_split(dataset, 2, axis=1)
    dataset_1 = features_split[0]
    dataset_2 = features_split[1]

    # 获取每个子集的样本数量和特征数量
    (num_examples_1, num_features_1) = dataset_1.shape
    (num_examples_2, num_features_2) = dataset_2.shape

    # 检查两个子集的样本数量是否相同
    if num_examples_1 != num_examples_2:
        raise ValueError('Can not generate polynomials for two sets with different number of rows')
    # 检查两个子集是否都有特征列
    if num_features_1 == 0 and num_features_2 == 0:
        raise ValueError('Can not generate polynomials for two sets with no columns')

    # 如果第一个子集没有特征列，使用第二个子集；反之亦然
    if num_features_1 == 0:
        dataset_1 = dataset_2
    elif num_features_2 == 0:
        dataset_2 = dataset_1

    #重新更新,获取最新的样本数量和特征数量
    (num_examples_1, num_features_1) = dataset_1.shape
    (num_examples_2, num_features_2) = dataset_2.shape


    # 确定要使用的特征数量，选择较小的特征数
    num_features = num_features_1 if num_features_1 < num_features_2 else num_features_2
    dataset_1 = dataset_1[:, :num_features]
    dataset_2 = dataset_2[:, :num_features]

    # 初始化一个空数组，用于存储生成的多项式特征
    polynomials = np.empty((num_examples_1, 0))

    # 生成多项式特征
    for i in range(1, polynomial_degree + 1):
        for j in range(i + 1):
            # 计算每个多项式特征
            polynomial_feature = (dataset_1 ** (i - j)) * (dataset_2 ** j)
            # 将新特征按列方向连接到 polynomials 数组中
            polynomials = np.concatenate((polynomials, polynomial_feature), axis=1)

    # 如果需要，进行标准化处理
    if normalize_data:
        polynomials = normalize(polynomials)[0]

    # 返回生成的多项式特征数组
    return polynomials

数据预处理模块¶

使用上面写的模块对数据进行预处理。

Prepare for training

"""Prepares the dataset for training"""

import numpy as np
from .normalize import normalize
from .generate_sinusoids import generate_sinusoids
from .generate_polynomials import generate_polynomials


def prepare_for_training(data, polynomial_degree=0, sinusoid_degree=0, normalize_data=True):

    # 计算样本总数
    num_examples = data.shape[0]

    data_processed = np.copy(data)

    # 预处理
    features_mean = 0
    features_deviation = 0
    data_normalized = data_processed
    if normalize_data:
        (
            data_normalized,
            features_mean,
            features_deviation
        ) = normalize(data_processed)

        data_processed = data_normalized

    # 特征变换sinusoidal
    if sinusoid_degree > 0:
        sinusoids = generate_sinusoids(data_normalized, sinusoid_degree)
        data_processed = np.concatenate((data_processed, sinusoids), axis=1)

    # 特征变换polynomial
    if polynomial_degree > 0:
        polynomials = generate_polynomials(data_normalized, polynomial_degree, normalize_data)
        data_processed = np.concatenate((data_processed, polynomials), axis=1)

    # 加一列1，为了计算常数项($$\theta_0$$)
    data_processed = np.hstack((np.ones((num_examples, 1)), data_processed))

    return data_processed, features_mean, features_deviation

类：LinearRegression 用于线性模型的机器学习¶

init初始化¶

import numpy as np

from linearstudy.utils.features import prepare_for_training

class LinearRegression:
    def __init__(self, data, labels, polynomial_degree=0, sinusoid_degree=0, normalize_data=True):
        # 准备训练数据，包括多项式特征、正弦特征和数据归一化
        (data_processed, features_mean, features_deviation) = prepare_for_training(data, polynomial_degree, sinusoid_degree, normalize_data)

        self.data = data_processed  # 处理后的数据
        self.labels = labels  # 标签,即真实值
        self.features_mean = features_mean  # 特征均值
        self.features_deviation = features_deviation  # 特征标准差
        self.polynomial_degree = polynomial_degree  # 多项式特征的度数
        self.sinusoid_degree = sinusoid_degree  # 正弦特征的度数
        self.normalize_data = normalize_data  # 是否归一化数据

        number = self.data.shape[1]  # 特征数量

        self.theta = np.zeros((number, 1))  # 初始化参数为零向量

预测函数(Hypothesis)¶

hypothesis函数主要是根据实际的x值与参数$\theta$y值

# 计算预测值
    def hypothesis(data, theta):
        predictions = np.dot(data, theta)  # 线性回归的预测值
        return predictions

使用全部样本数据更新$\theta$(Compute_gradient)¶

数学公式如下(正如我们在这里提到的)：

\[ \theta = \theta - \alpha \cdot \frac{1}{m} \cdot X^T (X\theta - y) \]

其中：

$\theta$ 为参数向量，
$\alpha$ 为学习率，
$m$ 为样本数量，
$X$ 为数据矩阵，
$y$ 为标签向量。

在代码中，compute_gradient 函数通过以下步骤实现梯度下降：

计算预测值：

predictions = LinearRegression.hypothesis(self.data, self.theta)

使用当前参数 $\theta$ 计算预测值。

计算预测误差：
```
delta = predictions - self.labels
```
预测值与实际标签之间的差异。

更新参数：

theta = theta - alpha * (1.0 / num_examples) * np.dot(delta.T, self.data).T
self.theta = theta

根据梯度下降公式更新参数 $\theta$。

汇总

# 梯度下降的计算，使用矩阵一次性使用所有样本的数据
def compute_gradient(self, alpha):
    num_examples = self.data.shape[0]  # 样本数量
    predictions = LinearRegression.hypothesis(self.data, self.theta)  # 预测值
    delta = predictions - self.labels  # 预测误差
    theta = self.theta
    theta = theta - alpha * (1.0 / num_examples) * np.dot(delta.T, self.data).T  # 更新参数
     self.theta = theta

损失函数的计算(Compute_cost)¶

通过计算损失函数并绘图可以帮助我们可视化训练的过程

def compute_cost(self, data, labels):
    num_examples = data.shape[0]  # 样本数量
    predictions = LinearRegression.hypothesis(data, self.theta)  # 预测值
    cost = (1.0 / (2 * num_examples)) * np.sum(np.square(predictions - labels))  # 均方误差
    return cost

使用梯度下降法并记录损失值(Gradient_descent)¶

def gradient_descent(self, alpha, iterations):
    # 梯度下降法
    loss = []
    for _ in range(iterations):
        self.compute_gradient(alpha)  # 计算梯度并更新参数
        loss.append(self.compute_cost(self.data, self.labels))  # 记录损失值
    return loss

Train¶

 def train(self, alpha, iterations=500):
    # 训练模型，使用梯度下降法
    cost_history = self.gradient_descent(alpha, iterations)
    return cost_history, self.theta

Get_cost¶

def get_cost(self, data, labels):
    # 获取给定数据的损失值
    data_processed, _, _ = prepare_for_training(data, self.polynomial_degree, self.sinusoid_degree, self.normalize_data)
    return self.compute_cost(data_processed, labels)

Predict¶

def predict(self, data):
    # 预测给定数据的结果
    data_processed, _, _ = prepare_for_training(data, self.polynomial_degree, self.sinusoid_degree, self.normalize_data)
    return LinearRegression.hypothesis(data_processed, self.theta)

使用实际数据集实战¶

实战一：只对一个自变量进行预测(Economy..GDP.per.Capita.)¶

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from linear import LinearRegression

data =pd.read_csv('linearstudy/data/world-happiness-report-2017.csv')

train_data =  data.sample(frac=0.8, random_state=200)
# 得到测试数据，drop方法是删除指定行的数据，这里是删除训练数据，得到测试数据
test_data = data.drop(train_data.index)

x_train = train_data[['Economy..GDP.per.Capita.']].values


y_train = train_data[['Happiness.Score']].values

x_test = test_data[['Economy..GDP.per.Capita.']].values

y_test = test_data[['Happiness.Score']].values

num_iterations = 500

alpha = 0.01

linear_regression = LinearRegression(x_train, y_train, polynomial_degree=1, normalize_data=True)

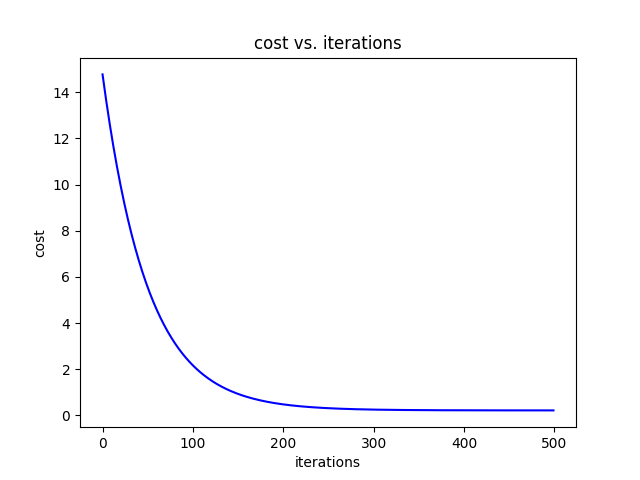
(cost,theta) = linear_regression.train(alpha, num_iterations)

print(f"开始时的损失值：{cost[0]}")

print(f"结束时的损失值：{cost[-1]}")

plt.plot(range(num_iterations), cost, color='blue')

plt.xlabel('iterations')

plt.ylabel('cost')

plt.title('cost vs. iterations')

plt.show()

predictions_nums = 100

x_predictions = np.linspace(x_test.min(), x_test.max(), predictions_nums).reshape(-1, 1)

y_predictions = linear_regression.predict(x_predictions)

plt.scatter(x_test, y_test, color='blue')

plt.scatter(x_train, y_train, color='red')

plt.plot(x_predictions, y_predictions, color='green')

plt.xlabel('Economy..GDP.per.Capita.')

plt.ylabel('Happiness.Score')

plt.title('Economy..GDP.per.Capita. vs. Happiness.Score')

plt.show()

Loss

从一开始14.766786065652582到最后0.2202886718845709

实战二：对两个自变量同时进行预测¶

其实在我们一开始写的文件中就已经处理了多个自变量的情况。比如在init中，

number = self.data.shape[1] # 特征数量

self.theta = np.zeros((number, 1)) # 初始化参数为零向量>

因此我们只要多取一列数据即可

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from linear import LinearRegression
data =pd.read_csv('linearstudy/data/world-happiness-report-2017.csv')

train_data =  data.sample(frac=0.8, random_state=200)
# 得到测试数据，drop方法是删除指定行的数据，这里是删除训练数据，得到测试数据
test_data = data.drop(train_data.index)

x_train = train_data[['Economy..GDP.per.Capita.','Freedom']].values

y_train = train_data['Happiness.Score'].values

x_test = test_data[['Economy..GDP.per.Capita.','Freedom']].values

y_test = test_data['Happiness.Score'].values


num_iterations = 500

alpha = 0.01

linear_regression = LinearRegression(x_train, y_train, polynomial_degree=1, normalize_data=True)

(cost,theta) = linear_regression.train(alpha, num_iterations)

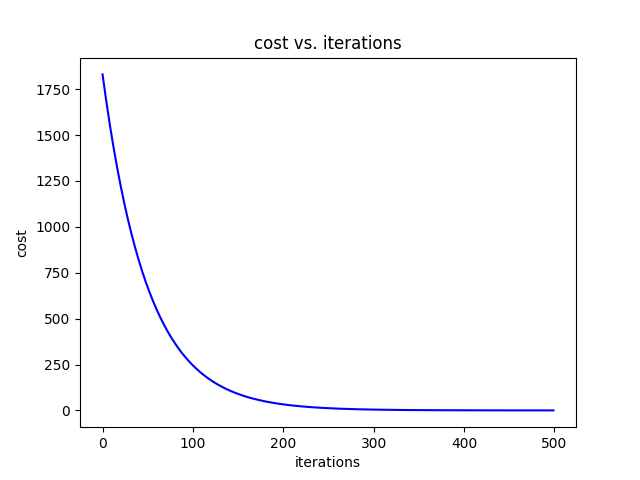
print(f"开始时的损失值：{cost[0]}")

print(f"结束时的损失值：{cost[-1]}")

plt.plot(range(num_iterations), cost, color='blue')

plt.xlabel('iterations')

plt.ylabel('cost')

plt.title('cost vs. iterations')

plt.show()

Loss

从一开始的1830.5394689767786到最后0.08063123386406645

所以我们可以看到，用两个自变量是比一个自变量训练效果好的

非线性回归¶

在上面的联系中，我们在训练$\theta$时都是默认x的次数是一次，也就是因变量与自变量的关系是线性的。下面是当我们假设因变量和自变量关系是非线性的情况。

读取数据¶

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from linear import LinearRegression

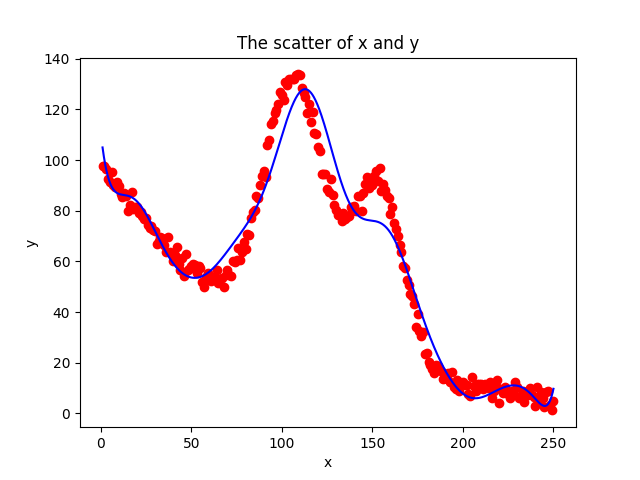
data = pd.read_csv('linearstudy/data/non-linear-regression-x-y.csv')

x=data['x'].values.reshape(data.shape[0],1)

y=data['y'].values.reshape(data.shape[0],1)

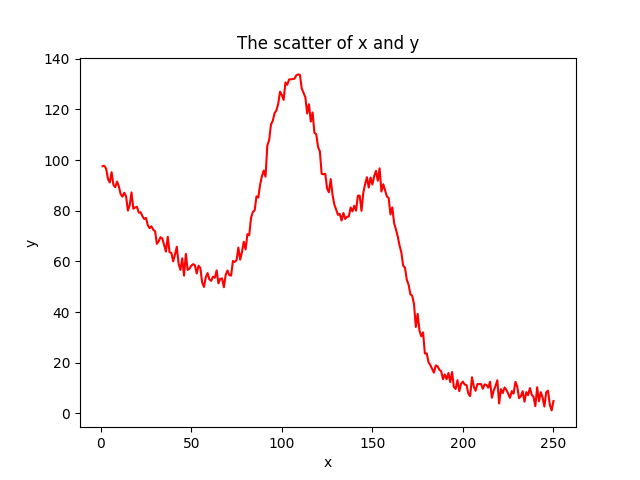
plt.plot(x, y,'r')

plt.xlabel('x')

plt.ylabel('y')

plt.title('The scatter of x and y')

plt.show()

数据图

做非线性处理¶

iterations = 50000

alpha = 0.01

polynomial_degree = 15

normalize_data = True

sinusoid_degree = 15

linear_regression = LinearRegression(x, y, polynomial_degree, sinusoid_degree,normalize_data )

在上述代码中：

多项式次数 (polynomial_degree = 15)：将原始特征扩展为15次多项式，有助于捕捉数据中的高次非线性关系.
正弦波次数 (sinusoid_degree = 15)：引入15个不同频率的正弦函数，增强模型对周期性模式的识别能力。

训练¶

(cost_history,theta) = linear_regression.train(alpha, iterations)

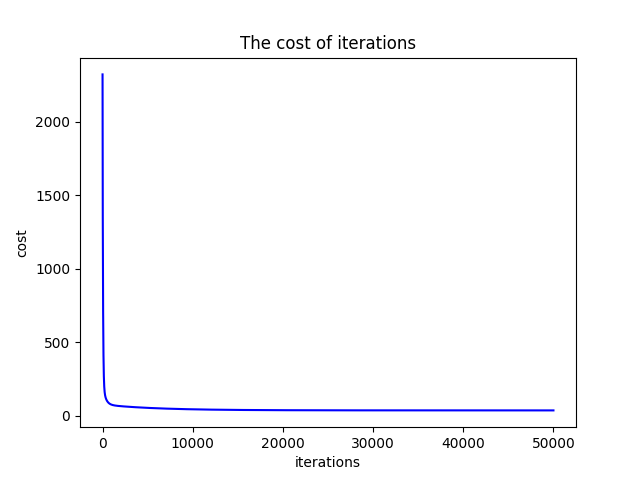
print(f'开始损失值: {cost_history[0]}')

print(f'结束损失值: {cost_history[-1]}')

plt.plot(range(iterations), cost_history, 'b')

plt.xlabel('iterations')

plt.ylabel('cost')

plt.title('The cost of iterations')

plt.show()

predicton_nums = 1000

x_pred = np.linspace(x.min(), x.max(), predicton_nums).reshape(predicton_nums, 1)

y_pred = linear_regression.predict(x_pred)

plt.scatter(x, y, c='r')

plt.plot(x_pred, y_pred, 'b')

plt.xlabel('x')

plt.ylabel('y')

plt.title('The scatter of x and y')

plt.show()

结果

Loss图拟合图

损失从一开始的2322.5164294103674降到最后35.110714989706445

模型评估¶

Sklearn¶

Sklearn库是一个功能强大的机器学习库，提供了丰富的算法和工具用于数据预处理、特征选择、模型训练和评估。

安装¶

可以使用以下命令通过pip安装scikit-learn：

pip install scikit-learn

或者在虚拟环境中

conda install scikit-learn

常用模块¶

linear_model: 线性回归、逻辑回归等模型
tree: 决策树
ensemble: 集成方法，如随机森林、梯度提升
preprocessing: 数据预处理工具
model_selection: 模型选择与验证

示例：线性回归¶

from sklearn.linear_model import LinearRegression
import numpy as np

# 准备数据
X = np.array([[1], [2], [3], [4], [5]])
y = np.array([2, 4, 6, 8, 10])

# 创建模型
model = LinearRegression()

# 训练模型
model.fit(X, y)

# 进行预测
predictions = model.predict([[6]])
print(predictions)  # 输出: [12.]

数据集的交叉验证¶

当我们拿到一个数据集时，需要进行切分。

首先，将数据集分为训练集和测试集，训练集用于训练模型，测试集用于评估模型的性能。

然而，在训练中，我们也常常需要对模型的性能进行评估，但是又不可能拿测试集来评估，因为这样会导致模型对测试集过拟合。因此，我们就需要在训练集内部进行切分，这就是交叉验证。

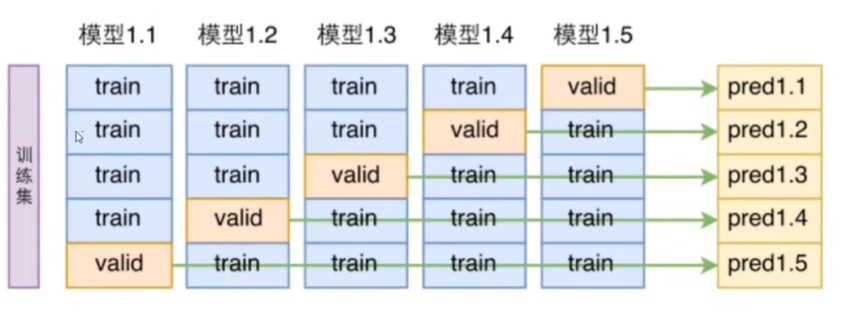
例如，我们可以将训练集分为5份，用1，2，3，4份训练模型，用第5份来评估模型的性能。然而，第5份数据可能比较复杂或者其他等等，不具有突出代表性，因此我们可以再用1，2，3，5份训练模型，用第4份来评估模型的性能，以此类推，我们可以得到5个模型，5个评估结果，最后取平均值。

因此，一个数据集的架构是:

训练集: 用于训练模型
验证集: 用于调整模型的超参数
测试集: 用于评估模型的性能

在sklearn中，就有交叉验证的库可以调用：

cross_validation

import numpy as np  # 导入numpy库用于数值计算
import os  # 导入os库用于操作系统相关功能
import matplotlib.pyplot as plt  # 导入matplotlib用于绘图
import warnings  # 导入warnings库用于控制警告信息
from sklearn.datasets import fetch_openml  # 从sklearn.datasets导入fetch_openml函数用于获取数据集
import joblib  # 导入joblib用于数据的持久化存储
from sklearn.model_selection import cross_val_score  # 导入cross_val_score用于交叉验证
from sklearn.linear_model import SGDClassifier  # 导入SGDClassifier用于分类模型

# 忽略所有警告信息
warnings.filterwarnings("ignore")

# 设置随机种子以确保结果可重复
np.random.seed(42)

# 定义数据集的保存路径
data_path = 'mnist_784.pkl'

# 检查本地是否存在数据集文件
if os.path.exists(data_path):
    mnist = joblib.load(data_path)  # 加载本地数据集
    print("加载本地数据集")
else:
    # 如果本地不存在，则从OpenML下载MNIST数据集
    mnist = fetch_openml('mnist_784', version=1, as_frame=False, parser='auto')
    joblib.dump(mnist, data_path)  # 保存下载的数据集到本地
    print("下载并保存数据集")

# 将特征数据转换为float64类型
X = mnist.data.astype('float64')
# 将目标标签转换为int32类型
y = mnist.target.astype('int32')

# 划分训练集和测试集，前60000个样本用于训练，后10000个样本用于测试
X_train, X_test = X[:60000], X[60000:]
y_train, y_test = y[:60000], y[60000:]

# 打印训练集和测试集的形状信息
print("数据集形状:")
print(f"X_train: {X_train.shape}, X_test: {X_test.shape}")
print(f"y_train: {y_train.shape}, y_test: {y_test.shape}")

# 生成一个0到60000的随机排列索引
shuffle_index = np.random.permutation(60000)

# 根据随机索引打乱训练集的顺序
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]

# 实例化SGD分类器，设置最大迭代次数、容忍度和随机状态
sgd_clf = SGDClassifier(max_iter=10000, tol=1e-3, random_state=42)

# 创建一个二元目标变量，仅标记为5的样本为True，其余为False
y_train_5 = (y_train == 5)

# 使用训练数据拟合SGD分类器
sgd_clf.fit(X_train, y_train_5)

# 打印交叉验证的准确率
print("交叉验证准确率:")

# 进行3折(把训练集拆分为3份)交叉验证，计算准确率
accuracy = cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring='accuracy')

# 输出交叉验证的结果
print(accuracy)

命令行输出:

加载本地数据集
数据集形状:
X_train: (60000, 784), X_test: (10000, 784)
y_train: (60000,), y_test: (10000,)
交叉验证准确率:
[0.9681  0.95655 0.95515]

混淆矩阵¶

混淆矩阵一般用于评估分类模型的性能，它是一个二维矩阵，用于展示模型的预测结果和真实标签之间的关系。一般的结构为：

\[ \begin{array}{|c|c|} \hline \text{真实类别} & \text{预测类别} \\ \hline \text{真负例} & \text{假正例} \\ \text{假负例} & \text{真正例} \\ \hline \end{array} \]

混淆矩阵

import numpy as np  # 导入numpy库用于数值计算
import os  # 导入os库用于操作系统相关功能
import matplotlib.pyplot as plt  # 导入matplotlib用于绘图
import warnings  # 导入warnings库用于控制警告信息
from sklearn.datasets import fetch_openml  # 从sklearn.datasets导入fetch_openml函数用于获取数据集
import joblib  # 导入joblib用于数据的持久化存储
from sklearn.model_selection import cross_val_score  # 导入cross_val_score用于交叉验证
from sklearn.linear_model import SGDClassifier  # 导入SGDClassifier用于分类模型

# 忽略所有警告信息
warnings.filterwarnings("ignore")

# 设置随机种子以确保结果可重复
np.random.seed(42)

# 定义数据集的保存路径
data_path = 'mnist_784.pkl'

# 检查本地是否存在数据集文件
if os.path.exists(data_path):
    mnist = joblib.load(data_path)  # 加载本地数据集
    print("加载本地数据集")
else:
    # 如果本地不存在，则从OpenML下载MNIST数据集
    mnist = fetch_openml('mnist_784', version=1, as_frame=False, parser='auto')
    joblib.dump(mnist, data_path)  # 保存下载的数据集到本地
    print("下载并保存数据集")

# 将特征数据转换为float64类型
X = mnist.data.astype('float64')
# 将目标标签转换为int32类型
y = mnist.target.astype('int32')

# 划分训练集和测试集，前60000个样本用于训练，后10000个样本用于测试
X_train, X_test = X[:60000], X[60000:]
y_train, y_test = y[:60000], y[60000:]

# 生成一个0到60000的随机排列索引
shuffle_index = np.random.permutation(60000)

# 根据随机索引打乱训练集的顺序
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]

# 实例化SGD分类器，设置最大迭代次数、容忍度和随机状态
sgd_clf = SGDClassifier(max_iter=10000, tol=1e-3, random_state=42)

# 创建一个二元目标变量，仅标记为5的样本为True，其余为False
y_train_5 = (y_train == 5)

from sklearn.model_selection import cross_val_predict  # 导入cross_val_predict用于交叉验证预测

result = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)

from sklearn.metrics import confusion_matrix  # 导入confusion_matrix用于混淆矩阵计算

matrix = confusion_matrix(y_train_5, result)

print(f"混淆矩阵：\n{matrix}")

输出结果:

[[53124  1455]
 [  949  4472]]

53124代表非5的结果被成功识别，1455代表非5的结果被错误识别，949代表5的结果被错误识别，4472代表5的结果被成功识别。

Sklearn中的评估函数¶

accuracy_score: 计算准确率.

from sklearn.metrics import accuracy_score
accuracy = accuracy_score(y_train_5, result)
print(f"准确率: {accuracy}")

precision_score: 计算精确率.

from sklearn.metrics import precision_score
precision = precision_score(y_train_5, result)
print(f"精确率: {precision}")

recall_score: 计算召回率.

from sklearn.metrics import recall_score
recall = recall_score(y_train_5, result)
print(f"召回率: {recall}")

f1_score: 计算F1分数(精确率和召回率的调和平均值).

from sklearn.metrics import f1_score
f1 = f1_score(y_train_5, result)
print(f"F1分数: {f1}")

评估阈值¶

阈值指的是分类器的决策边界，当分类器的预测概率大于阈值时，样本被划分为正例，否则被划分为负例。在sklearn中，我们可以使用decision_function()方法获取分类器的决策分数。这个函数返回每个样本的分数，然后我们可以根据这个分数设置不同的阈值。

from sklearn.metrics import precision_recall_curve  # 导入precision_recall_curve用于计算精确率和召回率

# 获取分类器的决策分数

scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method='decision_function')

# 计算精确率和召回率

precisions, recalls, thresholds = precision_recall_curve(y_train_5, scores)

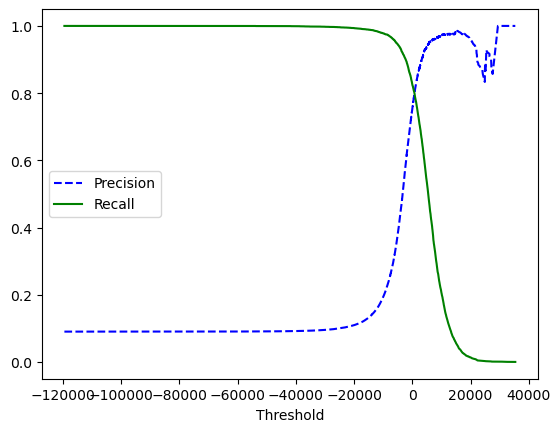
# 绘制精确率和召回率曲线

plt.plot(thresholds, precisions[:-1], 'b--', label='Precision')

plt.plot(thresholds, recalls[:-1], 'g-', label='Recall')

plt.xlabel('Threshold')

plt.legend()

plt.show()

阈值越大，精确率越高，召回率越低，反之亦然。

ROC曲线¶

ROC曲线也是一种用于评估二元分类器(就像这里识别某个数字是不是5)性能的工具，它展示了真正例率(TPR)和假正例率(FPR)之间的关系。TPR是指正确识别正例的比例，FPR是指错误识别负例的比例。ROC曲线的横轴是FPR，纵轴是TPR。

from sklearn.metrics import roc_curve  # 导入roc_curve用于计算ROC曲线

# 计算ROC曲线

fpr, tpr, thresholds = roc_curve(y_train_5, scores)

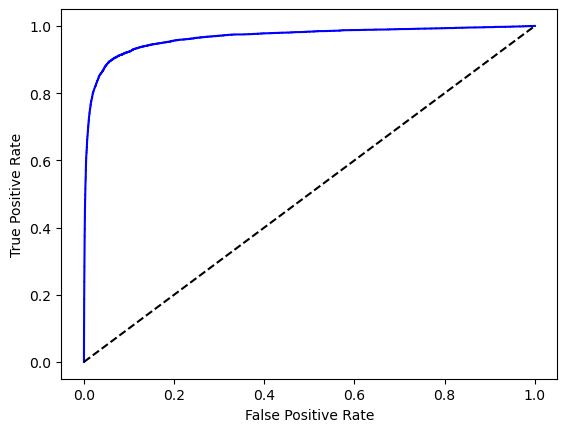
# 绘制ROC曲线

plt.plot(fpr, tpr, 'b-')

plt.plot([0, 1], [0, 1], 'k--')

plt.xlabel('False Positive Rate')

plt.ylabel('True Positive Rate')

plt.show()

这里理想的状态是ROC曲线尽可能地靠近左上角，即FPR为0，TPR为1。

常用的评估方法是计算ROC曲线下的面积(AUC)，AUC越接近1，分类器的性能越好。AUC为0.5意味着和纯随机分类没什么区别。

from sklearn.metrics import roc_auc_score  # 导入roc_auc_score用于计算AUC

# 计算AUC

auc = roc_auc_score(y_train_5, scores)

print(f"AUC: {auc}")