均摊分析¶
约 554 个字 2 张图片 预计阅读时间 3 分钟
参考资料
本篇目参考资料:
均摊分析(Amortized Analysis)是一种分析算法复杂度的方法,旨在计算在一系列操作中每个操作的平均代价。这种分析方法特别适用于那些在最坏情况下单个操作代价很高,但在一系列操作中代价较低的算法。
- 均摊分析的常用方法包括:
- 聚合分析(Aggregate Analysis):计算一系列操作的总代价,然后除以操作次数。
- 记账法(Accounting method) : 执行花费较低的operations时先存credit未雨绸缪, 供未来花费较高的operations使用。对每个操作定义一个合法的平摊成本(amortized cost) .假设\(c_i\)为第i个操作的actual cost,\(\hat{c_i}\)为第i个操作的amortized cost.若 \(c_i < \hat{c_i}\),则credit=\(\hat{c_i}-c_i\),我们把credit存起来(deposited),未来可以提取(withdraw) 。反之就是提取credit.总之,最后的credit需要\(\geq 0\),也即\(\sum_{i=1}^{n} \hat{c_i} \geq \sum_{i=1}^{n} c_i\)
- 势能法(Potential Method):引入一个势能函数来表示数据结构的潜在能量变化,通过势能变化来分析操作代价。
- 数学公式:
- 聚合分析:T(n) = O(f(n)),其中T(n)是n次操作的总代价,f(n)是一个函数。
- 均摊代价法:\(c_i \leq \hat{c_i}\),其中\(c_i\)是第i次操作的均摊代价。
- 势能法:\(c_i + Φ(D_i) - Φ(D_{i-1}) = \hat{c_i}\),其中\(c_i\)是第i次操作的实际代价,Φ是势能函数,\(D_i\)是第i次操作后的数据结构状态。因此\(\sum_{i=1}^{n}\hat{c_i} = \sum_{i=1}^{n} c_i +\Phi(D_n)-\Phi(D_{1})\)
在这里我们主要介绍势能法。
势能法¶
一言以蔽之
势能函数的核心就两句话:
-
尽量使初始状态的势能最小
-
对于实际开销大的步骤,要通过势能函数使\(\hat{c_i}\)小下来
例子¶
栈¶
假设我们现在有一个栈,可以进行如下操作:
-
push一个元素,代价1
-
pop一个元素,代价1
-
Multipop
k个元素,代价k
现在我们来思考一个势能函数,能够满足上面的要求。
势能函数的核心就两句话:
尽量使初始状态的势能最小
对于实际开销大的步骤,要通过势能函数使\(\hat{c_i}\)小下来
开销最大的步骤明显是Multipop,那么要使它的\(\hat{c_i}\)降下来,我们必须考虑一个势能函数使得\(\Phi(D_i)<<\Phi(D_{i-1})\),同时还要满足初始时整个结构的势能最小。欸,我们想到,可以定义\(\Phi(D_i)=sizeof(D_i),sizeof(D_i)\)指\(D_i\)下栈的元素个数。分析如下:
-
push:\(\hat{c_i}=c_i+\Phi(D_i)-\Phi(D_{i-1})=1+1=2\)
-
pop:\(\hat{c_i}=c_i+\Phi(D_i)-\Phi(D_{i-1})=1 - 1=0\)
-
Multipop:\(\hat{c_i}=c_i+\Phi(D_i)-\Phi(D_{i-1})=k-k=0\)
则\(\sum_{i=1}^n \hat{c_i}=\sum_{i=1}^n O(1)=O(n) \geq \sum_{i=1}^{n} c_i,故T_{amortized}=\frac{O(n)}{n}=O(1)\)
Splay Tree¶
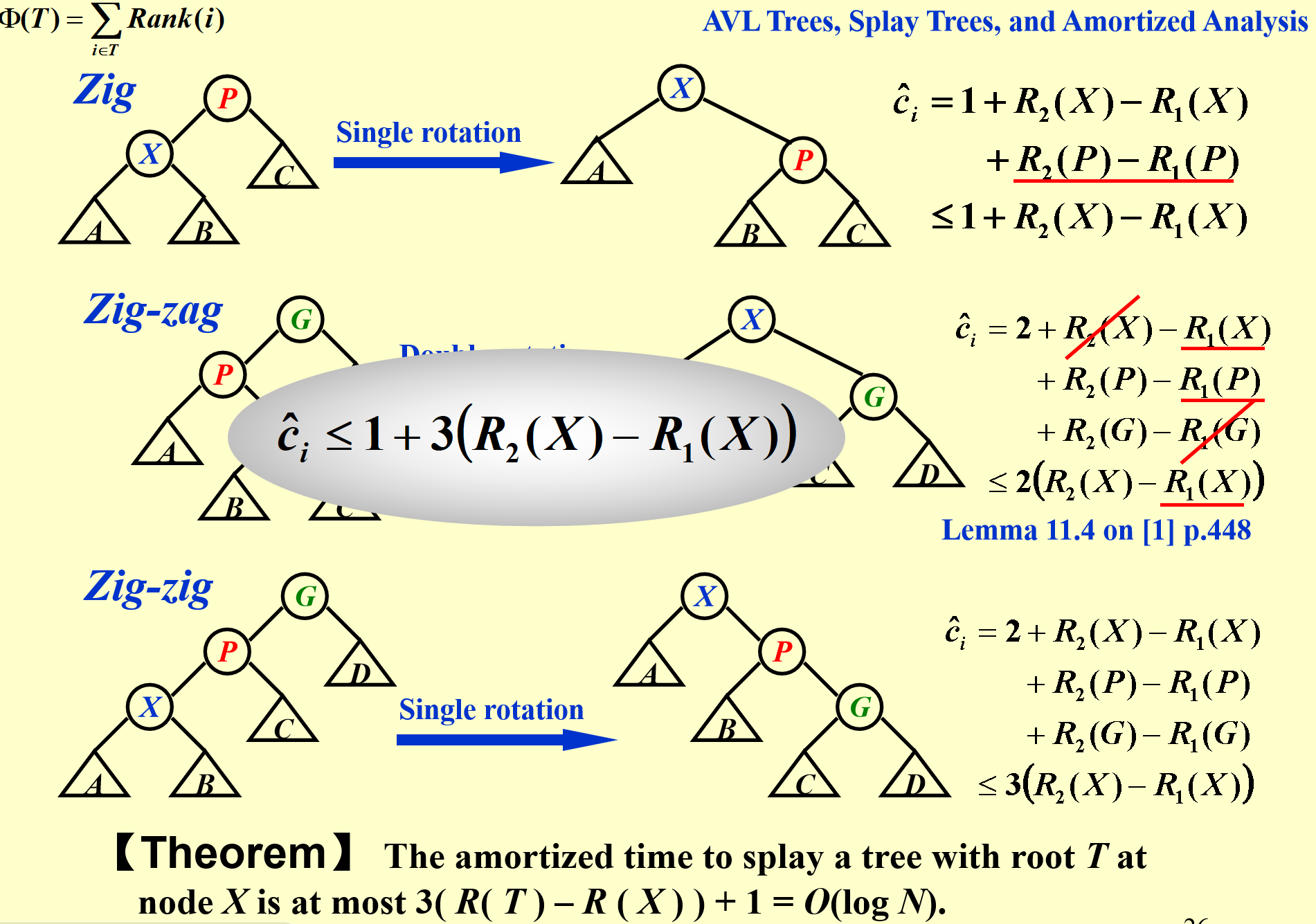
Splay Tree的三个操作分析起来有点复杂,并且包含了一些数学放缩,因此在这里不涉及了,放一张PPT上的图。
例题¶
题目
解析
先分析所有操作:
-
Available Block insert:开销1
-
Inadequate Block insert and move:开销k+1 再次,牢记势能函数的核心:
势能函数的核心就两句话:
-
尽量使初始状态的势能最小
-
对于实际开销大的步骤,要通过势能函数使\(\hat{c_i}\)小下来.
-
先来看第一条原则
尽量使初始状态的势能最小
可以直接排除掉B选项,C我感觉也可以排,但是说不清,先留着。然后再看这个结构开销最大的操作是Inadequate Block insert and move,因此我们的势能函数需要满足的特点是:在扩容后\(\Phi(D_i)\)大大减少,这时就可以看出D选项的合理性了。再来具体分析。应用D选项的势能函数后:
-
Available Block insert:\(\hat{c_i}=c_i+\Phi(D_i)-\Phi(D_{i-1})=1+1=2\)
-
Inadequate Block insert and move:\(\hat{c_i}=c_i+\Phi(D_i)-\Phi(D_{i-1})=k+1 - k+1=2\)
则
故