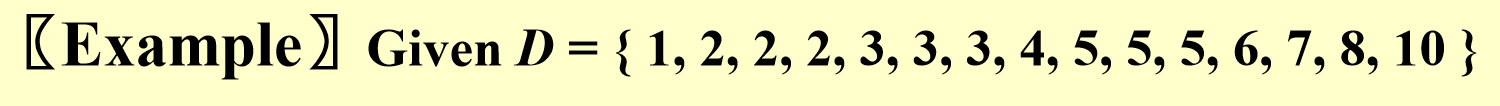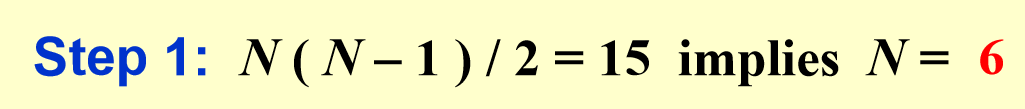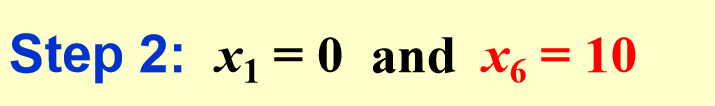Backtracking¶
约 264 个字 156 行代码 8 张图片 预计阅读时间 3 分钟
简要的介绍 from PPT¶
The basic idea is that suppose we have a partial solution ( \(x_1\), ... , \(x_i\) ) where each \(x_k \in S_k\) for \(1 \leq k \leq i < n\). First we add \(x_{i+1} \in S_{i+1}\) and check if ( \(x_1\), ... , \(x_i\), \(x_{i+1}\) ) satisfies the constrains. If the answer is “yes” we continue to add the next x, else we delete \(x_i\) and backtrack to the previous partial solution ( \(x_1\), ... , \(x_{i-1}\) ).
八皇后问题¶
八皇后问题是一个以国际象棋为背景的问题：如何能够在8×8的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？为了达到此目的，任两个皇后都不能处于同一条横行、纵行或斜线上。
为减少答案表示的复杂度，我们作如下规定：
答案表示
令答案\(S_i = {x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8}\),其中\(x_i\)表示第i行皇后所在的列数。这很显然是正确的，因为必然每一行都有且仅有一个皇后。
现在，我们来思考这个问题有哪些约束。
constrains
-
\(S_i\)有8位，每一位数字都是1-8之间的一个。这将答案个数缩减到\(8^8\)
-
$x_i \neq x_j $ if \(i \neq j\).这是显然的，因为不可能有两个皇后在同一列。答案缩减到\(8!\)
-
\(\frac{x_i-x_j}{i-j} \neq \pm 1\),这是为了确保对角线上不会攻击。
然后，我们就可以使用深度优先搜索的思想，来遍历所有可能，找到答案。
#include <stdio.h>
#define QUEENS 8 /* 皇后数量 */
#define IS_OUTPUT 1 /* (IS_OUTPUT=0 or 1)，Output用于选择是否输出具体解,为1输出，为0不输出 */
/* 定义辅助数组和变量 */
int A[QUEENS + 1], B[QUEENS * 3 + 1], C[QUEENS * 3 + 1], k[QUEENS + 1][QUEENS + 1];
int inc, *a = A, *b = B + QUEENS, *c = C;
/* a[j] 记录第 j 列是否有皇后。如果 a[j] 为 1，表示第 j 列已经有皇后；如果为 0，表示第 j 列没有皇后。
b[j - i] 记录从左上到右下的对角线是否有皇后。对角线的索引是 j - i，如果 b[j - i] 为 1，表示该对角线上已经有皇后；如果为 0，表示该对角线上没有皇后。
c[j + i] 记录从右上到左下的对角线是否有皇后。对角线的索引是 j + i，如果 c[j + i] 为 1，表示该对角线上已经有皇后；如果为 0，表示该对角线上没有皇后。
*/
/* 递归函数，用于在第i行放置皇后 */
void lay(int i) {
int j = 0, t, u;
/* 尝试在第i行的每一列放置皇后 */
while (++j <= QUEENS)
/* 检查当前位置是否安全（没有冲突） */
if (a[j] + b[j - i] + c[j + i] == 0) {
/* 放置皇后，并标记相关数组 */
k[i][j] = a[j] = b[j - i] = c[j + i] = 1;
/* 如果还没有放置完所有皇后，递归调用lay函数 */
if (i < QUEENS) lay(i + 1);
else {
/* 如果已经放置了所有皇后，增加解的数量 */
++inc;
/* 如果IS_OUTPUT为1，输出当前解 */
if (IS_OUTPUT) {
for (printf("(%d)\n", inc), u = QUEENS + 1; --u; printf("\n"))
for (t = QUEENS + 1; --t; ) k[t][u] ? printf("Q ") : printf("+ ");
printf("\n\n\n");
}
}
/* 回溯，撤销当前皇后的放置 */
a[j] = b[j - i] = c[j + i] = k[i][j] = 0;
}
}
/* 主函数 */
int main(void) {
/* 从第一行开始放置皇后 */
lay(1);
/* 输出总共找到的解的数量 */
printf("%d皇后共计%d个解\n", QUEENS, inc);
return 0;
}
The Turnpike Reconstruction Problem¶
公路重建问题（The Turnpike Reconstruction Problem）是一个经典的组合优化问题。其目标是根据给定的一组点之间的距离，重建这些点的原始位置。
问题描述¶
假设有 \(n\) 个点 \(x_1, x_2, ..., x_n\)，它们在一条直线上。已知这些点之间的所有两两距离 \(d_{ij} = |x_i - x_j|\)，其中 \(1 \leq i < j \leq n\)。（很显然，有 \(\frac{N(N-1)}{2}\) 个距离）公路重建问题要求根据这些距离重建点的原始位置。
数学描述¶
给定一个距离集合 \(D = \{d_{ij} | 1 \leq i < j \leq n\}\)，重建点集 \(X = \{x_1, x_2, ..., x_n\}\)，使得对于任意的 \(i, j\)，\(d_{ij} = |x_i - x_j|\)。我们假设离起点最近的点为\(x_1\),在坐标\(x=0\)处。
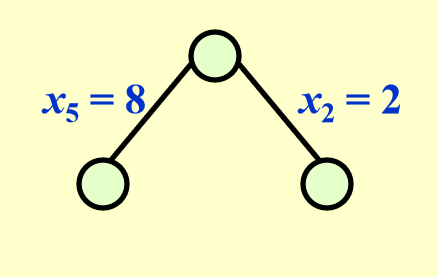
解题思路¶
例子
假设我们现在有一个距离集合
由距离得到点的个数
发现起始点和最远的点。
找到第二大的距离开始尝试。在本例中，第二大距离是8，有两种可能：
-
第二远的点\(x_5\)距离\(x_1\)为8
-
第二近的点距离\(x_6\)为8
由此画出一棵树。
之后不断尝试，检查距离是否满足条件即可。
代码实现¶
#include <iostream>
#include <vector>
#include <unordered_set>
#include <cmath>
#include <algorithm>
using namespace std;
int Find_Max(const unordered_set<int>& D) {
return *max_element(D.begin(), D.end());
}
bool Check(int value, const vector<int>& X, int N, int left, int right) {
for (int i = 1; i < left; i++) {
if (D.find(abs(value - X[i])) == D.end()) {
return false;
}
}
for (int i = right + 1; i <= N; i++) {
if (D.find(abs(value - X[i])) == D.end()) {
return false;
}
}
return true;
}
/* X[1]...X[left-1] and X[right+1]...X[N] are solved */
bool Reconstruct(vector<int>& X, unordered_set<int>& D, int N, int left, int right) {
if (D.empty()) {
return true;
}
int D_max = Find_Max(D);
bool Found = false;
// Option 1: X[right] = D_max
if (Check(D_max, X, N, left, right)) {
X[right] = D_max;
for (int i = 1; i < left; i++) {
D.erase(abs(X[right] - X[i]));
}
for (int i = right + 1; i <= N; i++) {
D.erase(abs(X[right] - X[i]));
}
Found = Reconstruct(X, D, N, left, right - 1);
if (!Found) {
for (int i = 1; i < left; i++) {
D.insert(abs(X[right] - X[i]));
}
for (int i = right + 1; i <= N; i++) {
D.insert(abs(X[right] - X[i]));
}
}
}
// Option 2: X[left] = X[N] - D_max
if (!Found) {
if (Check(X[N] - D_max, X, N, left, right)) {
X[left] = X[N] - D_max;
for (int i = 1; i < left; i++) {
D.erase(abs(X[left] - X[i]));
}
for (int i = right + 1; i <= N; i++) {
D.erase(abs(X[left] - X[i]));
}
Found = Reconstruct(X, D, N, left + 1, right);
if (!Found) {
for (int i = 1; i < left; i++) {
D.insert(abs(X[left] - X[i]));
}
for (int i = right + 1; i <= N; i++) {
D.insert(abs(X[left] - X[i]));
}
}
}
}
return Found;
}
int main() {
int n;
cout << "输入点的数量: ";
cin >> n;
int dist_count = n * (n - 1) / 2;
unordered_set<int> distances;
cout << "输入所有两两距离: ";
for (int i = 0; i < dist_count; i++) {
int d;
cin >> d;
distances.insert(d);
}
vector<int> points(n + 1);
points[1] = 0;
points[n] = *distances.rbegin();
if (Reconstruct(points, distances, n, 2, n - 1)) {
cout << "重建的点位置: ";
for (int i = 1; i <= n; i++) {
cout << points[i] << " ";
}
cout << endl;
} else {
cout << "无法重建点位置" << endl;
}
return 0;
}
总结¶
回溯算法的总体套路。
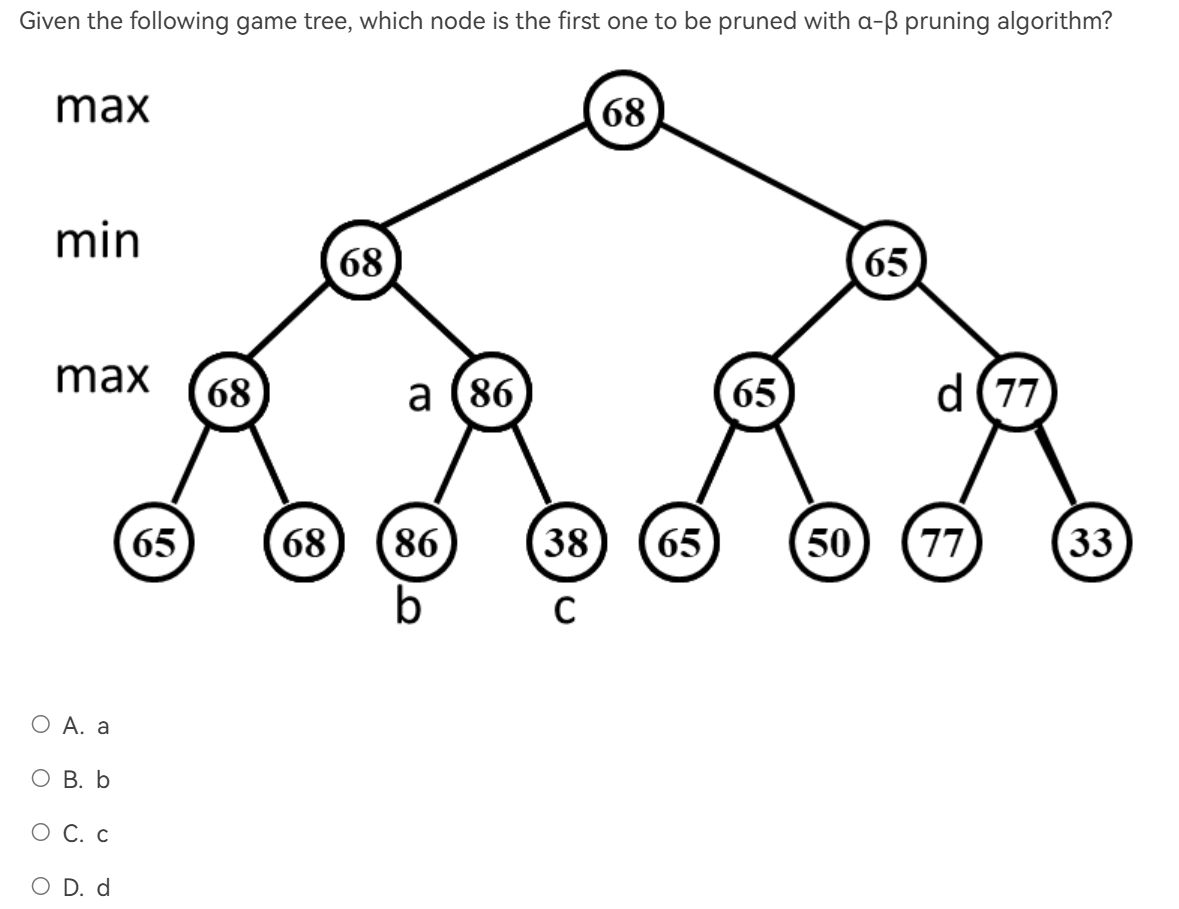
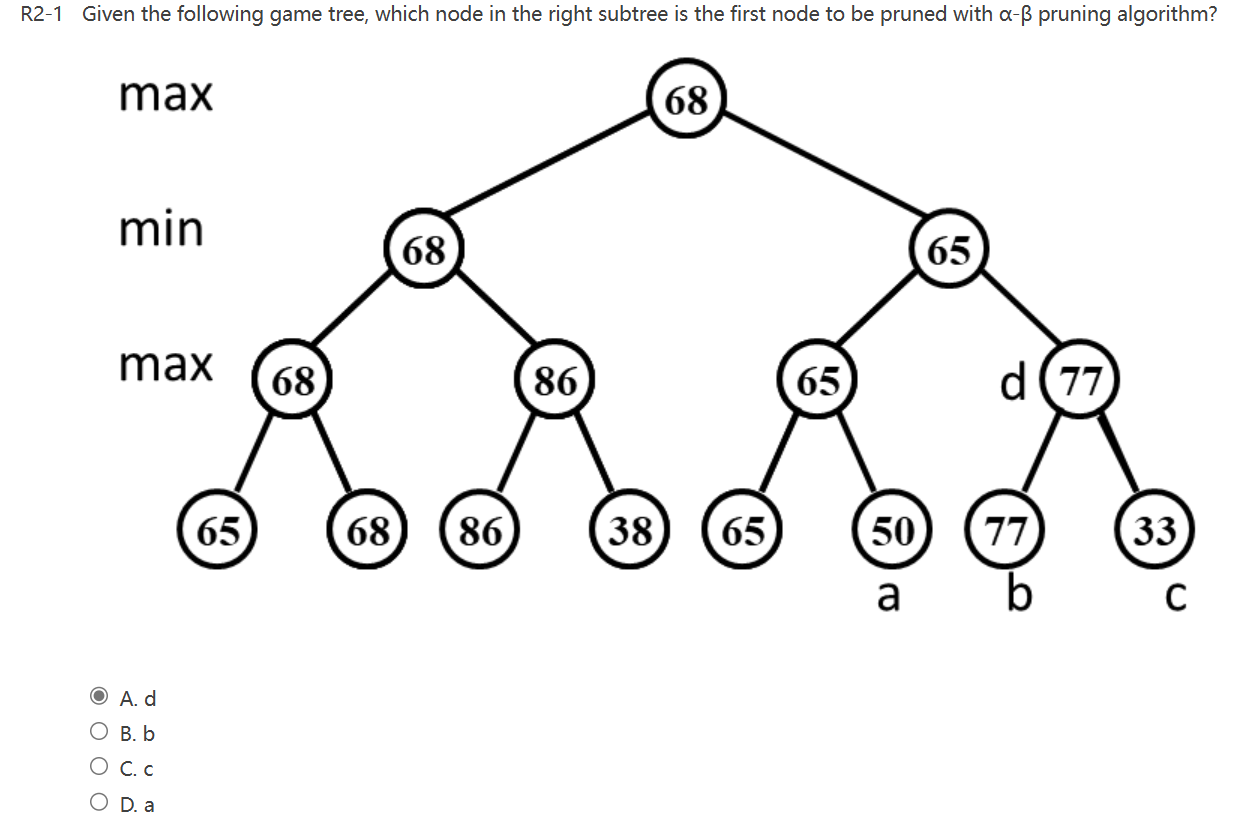
\(\alpha - \beta\)剪枝¶
我认为讲得很清楚的一篇帖子，还有oiwiki，有空(大概率不会)再码
例题¶
例题
解析
3-3=0，选B
解析
按照深度优先搜索的顺序，我们访问到a的父亲，此时a的父亲的\(\beta\)为68，而a的\(\alpha\)为86（先访问了b），此时\(\alpha > \beta\)，已经不会有意义了，所以不再需要访问c，也就是c被剪枝了。选C
解析
和上一道题一样，a肯定是有必要访问的，不然我们都不知道a的父亲会是多少。在访问了a之后，我们确定a的父亲是65，因此a的爷爷会取的值必然\(\leq 65\)。但是呢，在a的爷爷这一层我们取的是max，另一边是68，也就是绝对不可能取这一边了。因此d没必要访问，可以剪去。选A