Binomial Queue¶

约 883 个字 91 行代码 7 张图片预计阅读时间 6 分钟

资料

wiki:https://zh.wikipedia.org/wiki/%E4%BA%8C%E9%A1%B9%E5%A0%86

二项树定义与性质¶

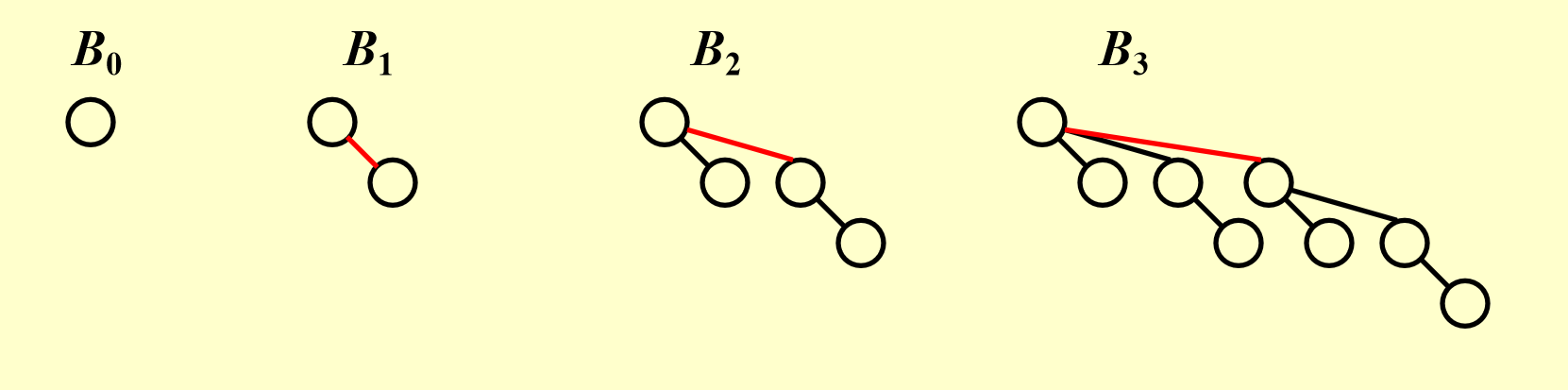
度数为0的二项树只包含一个节点
度数为k的二项树是由一颗度数为\(k-1\)的二项树直接插到另一颗度数为\(k-1\)的二项树根下，含有k个节点，共ingk层
度数为k的二项树有k个孩子，分别为度数为0，1，...,k-1的二项树
度数为k的二项树在第d层有\(C_{k}^{d}\)个节点

例子

可以看出上述所有性质，比如度为3的二项树各层节点数为1，3，3，1，可以联想到杨辉三角的第三层。

二项队列¶

概念¶

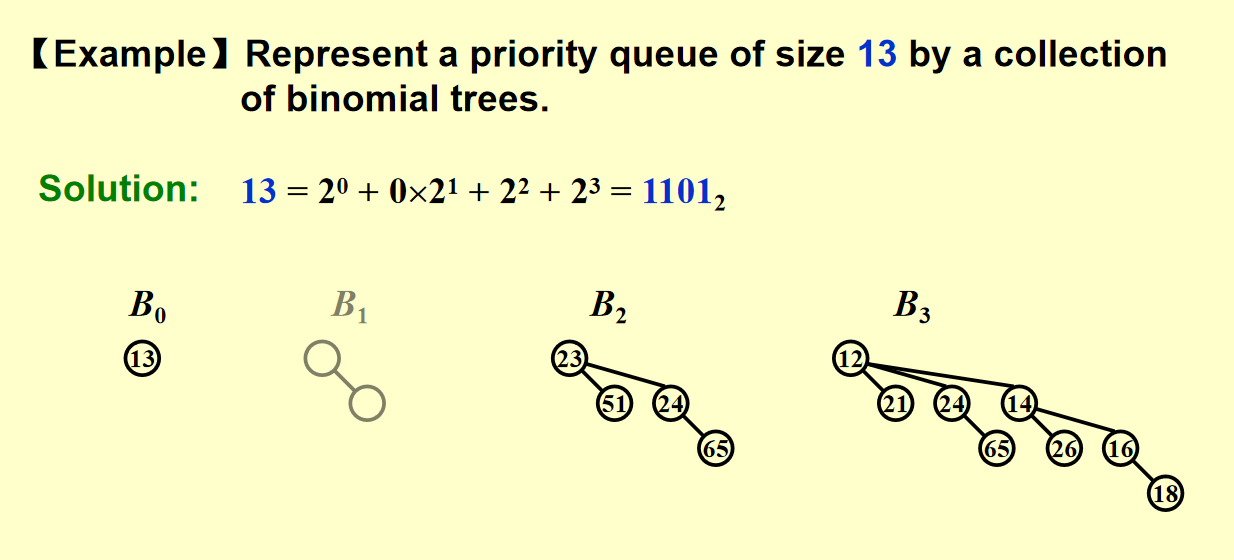
二项队列就是有一堆二项树组成，每个二项树满足堆的性质(大顶堆/小顶堆)。

例子

例如，如果一个二项队列有13个元素，\(13=(1101)_2\),即由一颗度为0，一颗度为2，一颗度为3的二项树组成

操作¶

FindMin¶

可以用一个指针标记最值。因此时间复杂度可以是\(O(1)\)。如果没有标记，遍历根的话，是\(O(\log(N))\)

Merge¶

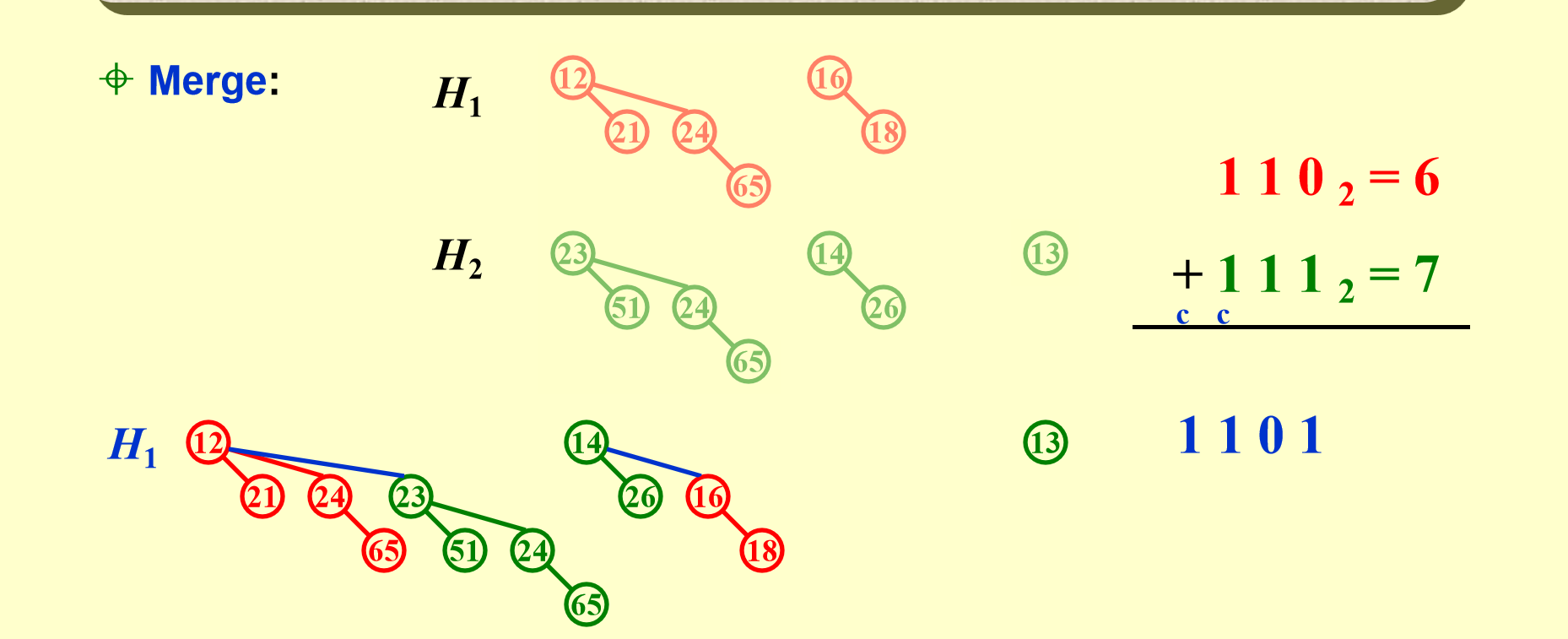
两个二项队列的合并就是把度相同的二项树合并。

其实也可以看成是二进制数相加

因此就有三棵树，度分别为3，2，0，由此我们也可以推出合并的时间复杂度是\(O(\log(N))\),因为二进制有\(\log(N)\)位

例子

Insert¶

特殊的merge.我们想使用均摊分析法，证明N个连续的Insert可以是\(O(N)\)的时间复杂度

聚合分析法¶

发现

如果我们把二项队列看成一个二进制数...

n=....0,cost=1
n=....01,cost=2
n=....011,cost=3
n=....0111,cost=4

我们发现，开销实际上就是根据低位连续的1的个数来决定。那么N步插入，每种情况各出现多少次呢？

发现

对于n=....0的情况，有一半的插入情况是这样
对于n=....01的情况，有\(\frac{1}{2} * \frac{1}{2}=\frac{1}{4}\)
...

因此，总开销为\(\frac{n}{2}*1+\frac{n}{4}*2+...=2N\)

均摊下来就是常数时间。

势能法¶

我们不妨思考，哪一步的开销最大？显然是当发生进位，也即我们需要删除树并合并树的情况，不然，直接创造树即可。根据均摊分析的原则，让开销大的步骤尽可能小下来，我们作如下规定：

前提

\(\hat{c_i}=c_i+\Phi(D_i)-\Phi(D_{i-1})\)
\(\Phi(D_i)=\)number of trees after the ith insertion

如果某步Insertion\(c_i\)的cost为k，那么必然是除了一次创建以外，合并了k-1次，也即树的个数减少了\(k-2\)(第一步合并后\(\Phi(D_i)=\Phi(D_{i-1})\))

因此\(\hat{c_i}=c_i+\Phi(D_i)-\Phi(D_{i-1})=k-(k-2)=2\)

\(\therefore T_{\text{amortized}}=\frac{2N}{N}=2\)

DeleteMin¶

以下步骤：

FindMin:\(O(\log(N))\)
remove(移除最小值作为根的树):\(O(1)\)
移除根，原来的树被拆分：\(O(\log(N))\)
merge:\(O(\log(N))\)

code¶

数据结构定义¶

数据结构

typedef int ElementType
typedef struct BinNode *Position;
typedef struct Collection *BinQueue;
typedef struct BinNode *BinTree;  /* missing from p.176 */

struct BinNode 
{ 
    ElementType     Element;
    Position        LeftChild;
    Position        NextSibling;
} ;

struct Collection 
{ 
    int         CurrentSize;  /* total number of nodes */
    BinTree TheTrees[ MaxTrees ];
} ;

Merge¶

同大小的树合并

BinTree CombineTrees( BinTree T1, BinTree T2 )
{  /* merge equal-sized T1 and T2 */
    if ( T1->Element > T2->Element )
        /* attach the larger one to the smaller one */
        return CombineTrees( T2, T1 );
    /* insert T2 to the front of the children list of T1 */
    T2->NextSibling = T1->LeftChild;
    T1->LeftChild = T2;
    return T1;
}

总的合并

BinQueue  Merge( BinQueue H1, BinQueue H2 )
{   BinTree T1, T2, Carry = NULL;   
    int i, j;
    if ( H1->CurrentSize + H2-> CurrentSize > Capacity )  ErrorMessage();
    H1->CurrentSize += H2-> CurrentSize;
    for ( i=0, j=1; j<= H1->CurrentSize; i++, j*=2 ) {
        T1 = H1->TheTrees[i]; T2 = H2->TheTrees[i]; /*current trees */
        switch( 4*!!Carry + 2*!!T2 + !!T1 ) { 
        case 0: /* 000 */
        case 1: /* 001 */  break;   
        case 2: /* 010 */  H1->TheTrees[i] = T2; H2->TheTrees[i] = NULL; break;
        case 4: /* 100 */  H1->TheTrees[i] = Carry; Carry = NULL; break;
        case 3: /* 011 */  Carry = CombineTrees( T1, T2 );
                        H1->TheTrees[i] = H2->TheTrees[i] = NULL; break;
        case 5: /* 101 */  Carry = CombineTrees( T1, Carry );
                        H1->TheTrees[i] = NULL; break;
        case 6: /* 110 */  Carry = CombineTrees( T2, Carry );
                        H2->TheTrees[i] = NULL; break;
        case 7: /* 111 */  H1->TheTrees[i] = Carry; 
                        Carry = CombineTrees( T1, T2 ); 
                        H2->TheTrees[i] = NULL; break;
        } /* end switch */
    } /* end for-loop */
    return H1;
}

DeleteMin¶

DeleteMin

ElementType  DeleteMin( BinQueue H )
{   BinQueue DeletedQueue; 
    Position DeletedTree, OldRoot;
    ElementType MinItem = Infinity;  /* the minimum item to be returned */  
    int i, j, MinTree; /* MinTree is the index of the tree with the minimum item */

    if ( IsEmpty( H ) )  {  PrintErrorMessage();  return –Infinity; }

    for ( i = 0; i < MaxTrees; i++) {  /* Step 1: find the minimum item */
        if( H->TheTrees[i] && H->TheTrees[i]->Element < MinItem ) { 
        MinItem = H->TheTrees[i]->Element;  MinTree = i;    } /* end if */
    } /* end for-i-loop */
    DeletedTree = H->TheTrees[ MinTree ];  
    H->TheTrees[ MinTree ] = NULL;   /* Step 2: remove the MinTree from H => H’ */ 
    OldRoot = DeletedTree;   /* Step 3.1: remove the root */ 
    DeletedTree = DeletedTree->LeftChild;   free(OldRoot);
    DeletedQueue = Initialize();   /* Step 3.2: create H” */ 
    DeletedQueue->CurrentSize = ( 1<<MinTree ) – 1;  /* 2MinTree – 1 */
    for ( j = MinTree – 1; j >= 0; j – – ) {  
        DeletedQueue->TheTrees[j] = DeletedTree;
        DeletedTree = DeletedTree->NextSibling;
        DeletedQueue->TheTrees[j]->NextSibling = NULL;
    } /* end for-j-loop */
    H->CurrentSize  – = DeletedQueue->CurrentSize + 1;
    H = Merge( H, DeletedQueue ); /* Step 4: merge H’ and H” */ 
    return MinItem;
}

例题¶

例题

T1T2T3T4

解析

\((42)_{10}=(101010)_2\)

解析

均摊分析法，Insertion是\(O(1)\)

find-max比较难，肯定不是，findmin倒是有可能\(O(1)\)（指针标记）

merge和deletemin都是\(O(\log(N))\)

解析

D选项：4为根的\(B_2\)和2为根的\(B_2\)合并了。23就不用动了。

解析

C选项：29当然可以作为根，另外两个\(B_2\)去合并就行

Binomial Queue¶

二项树定义与性质¶

二项队列¶

概念¶

操作¶

FindMin¶

Merge¶

Insert¶

聚合分析法¶

势能法¶

DeleteMin¶

code¶

数据结构定义¶

Merge¶

DeleteMin¶

例题¶

评论