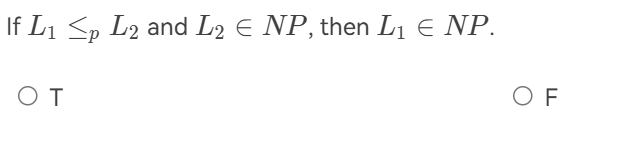NP Completeness¶
约 2195 个字 7 行代码 11 张图片 预计阅读时间 11 分钟
P与NP
P的意思是“Polynomial”,多项式时间可解决,
NP是“Nondeterministic Polynomial time”的缩写,指的是在非确定性多项式时间内可以验证解的问题集合。
Halting problem¶
Warning
Is it possible to have your C compiler detect all infinite loops?
答案是否
假设我们有这样的一个函数H(P,I),可以判断函数P在输入I是是否为死循环,如果是,返回1,不然返回0.
根据H我们可以构造一个U(P):
考虑U(U)的调用结果:
Tip
如果是死循环,则H(U,U)为1,进入break,我们在U(U)是死循环的基础上推出U(U)不是死循环。
不然,则进入死循环,我们在U(U)不是死循环的基础上推出U(U)是死循环。
综上所述,不存在这样的H,不然,我们总可以构造出一个U造成矛盾。
图灵机¶
Deterministic Turing Machine¶
确定性图灵机指的是机器根据指令前往一个特定的地方。
from PPT
A Deterministic Turing Machine executes one instruction at each point in time. Then depending on the instruction, it goes to the next unique instruction.
Nondeterministic Turing Machine¶
非确定型图灵机中,机器可以自由选择下一步做什么,并总是选择正确答案。
from PPT
A Nondeterministic Turing Machine is free to choose its next step from a finite set. And if one of these steps leads to a solution, it will always choose the correct one.
True NP!¶
一个问题是NP的,意味着虽然我们不知道能不能在多项式时间内找到它的解,但对于任何一个可能的解,我们可以在多项式时间内验证它是否是正确的。
Warning
Not all decidable problems are in NP. For example, consider the problem of determining whether a graph does not have a Hamiltonian cycle.
显然,
NP完全¶
NPC问题是NP问题里最"难"的问题。
polynomial reduce
问题的难度:如果我们能在多项式时间的复杂度内,将问题 A 转化为问题 B,则称问题 A 可以多项式时间归约(polynomial reduce)为 B,记为 $A \leq_p B $,表示 A 不会比 B 难。
那么,如果我们能证明任何一个NPC问题可以在多项式复杂度内解决,那么所有的NP问题都可以在多项式复杂度内解决,那么就有
Traveling salesman problem¶
Definition
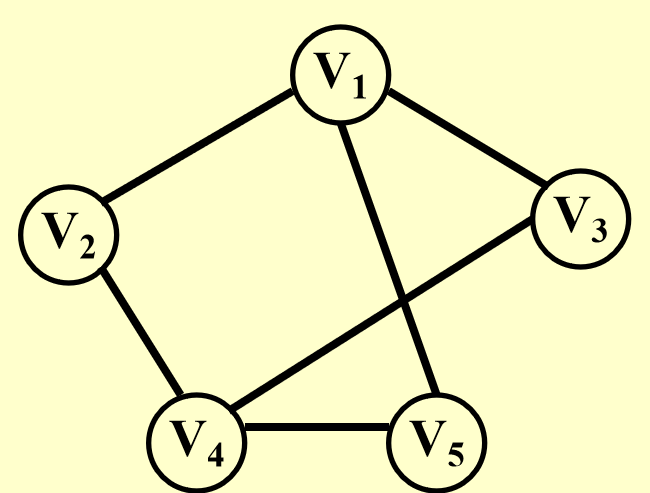
Given a graph G=(V, E), is there a simple cycle that visits all vertices?
Given a complete graph G=(V, E), with edge costs, and an integer K, is there a simple cycle that visits all vertices and has total cost \(\leq\) K?
如何证明TSP是一个NPC问题?
假设我们已经知道Hamiltonian cycle problem是一个NPC问题。
首先,TSP问题显然是一个NP问题,因为任何一个它的可能解,都可以在\(O(N)\)的时间范围内得到验证。
其次,对于任何一个回路是否有Hamiltonian cycle,我们可以作如下思考
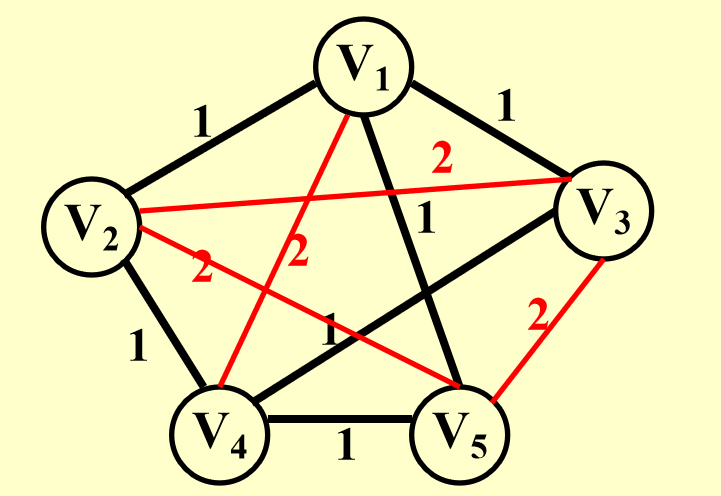
我们在把一个图拓展为完全图时,将图原来就有的边权值定义为1,新添加的边权值定义为2,那么对于原来的图是否有Hamiltonian cycle,就可以转换为拓展后的完全图在TSP问题上是否有解的问题(令K = |v|)。
由于完全图的边数为\(\frac{n(n+1)}{2}\),因此这个转换过程是多项式时间复杂度的。综上,我们从Hamiltonian cycle是NPC问题推出了TSP是NPC问题。
第一个NPC问题从何而来
The first problem that was proven to be NP-complete was the Satisfiability problem (Circuit-SAT): Input a boolean expression and ask if it has an assignment to the variables that gives the expression a value of 1.
Cook showed in 1971 that all the problems in NP could be polynomially transformed to Satisfiability. He proved it by solving this problem on a nondeterministic Turing machine in polynomial time.
Formal-language Theory¶
字母表¶
- 字母表(\(\Sigma\)):一个有限的符号集合。
语言¶
- 语言(\(L\)):由字母表 \(\Sigma\) 中符号组成的字符串集合。
- 空字符串:用 \(\varepsilon\) 表示。
- 空语言:用 \(\emptyset\) 表示。
- 所有字符串的语言:用 \(\Sigma^*\) 表示。
- 补集:\(L\) 的补集表示为 $ \Sigma ^* - L$。
语言的运算¶
-
连接:
- 两个语言 \(L_1\) 和 \(L_2\) 的连接是:
- \(L = \{ x_1x_2 \mid x_1 \in L_1 \text{ 且 } x_2 \in L_2 \}\)。
- 两个语言 \(L_1\) 和 \(L_2\) 的连接是:
-
闭包(克林星闭包,Kleene star):
- 语言 \(L\) 的闭包表示为 \(L^*\),定义为:
- \(L^* = \{\varepsilon\} \cup L \cup L^2 \cup L^3 \cup \dots\),
- 其中 \(L^k\) 是通过将 \(L\) 自身连接 \(k\) 次得到的语言。
- 语言 \(L\) 的闭包表示为 \(L^*\),定义为:
算法与语言的决定¶
- Accept:算法 \(A\) 接受字符串 \(x \in \{0, 1\}^*\) 当且仅当 \(A(x) = 1\)。
- Reject:算法 \(A\) 拒绝字符串 \(x\) 当且仅当 \(A(x) = 0\)。
- Decide:如果每一个属于语言 \(L\) 的二进制字符串都被算法 \(A\) 接受,并且每一个不属于 \(L\) 的二进制字符串都被算法 \(A\) 拒绝,那么算法 \(A\) 决定了语言 \(L\)。
- 为了接受一个语言,算法只需要处理属于 \(L\) 的字符串;但要决定一个语言,算法必须正确地接受或拒绝 \(\{0, 1\}^*\) 中的每一个字符串。
NP 类的语言¶
- 定义:一个语言 \(L\) 属于 NP,当且仅当存在一个双输入的多项式时间算法 \(A\) 和一个常数 \(c\),满足 $$ L = { x \in {0, 1}^* \mid \exists y \text{,且 } |y| = O(|x|^c) \text{ 且 } A(x, y) = 1 }。 $$ 换句话说,算法 \(A\) 在多项式时间内验证语言 \(L\)。
语言的多项式约化¶
L1 is polynomial-time reducible to a language L2 ( \(L1 \leq_P L2\) )
语言 \(L_1\) 可以多项式约化到语言 \(L_2\),当且仅当存在一个多项式时间算法 \(A\),使得对于所有的字符串 \(x\),\(x \in L_1\) 当且仅当 \(A(x) \in L_2\)。
Clique problem与Vertex cover problem¶
Clique problem¶
定义:给定一个无向图 \(G\) 和一个整数 \(k\),判断 \(G\) 中是否存在一个包含 \(k\) 个顶点的完全子图(clique)。
Vertex cover problem¶
定义:给定一个无向图 \(G\) 和一个整数 \(k\),判断 \(G\) 中是否存在一个包含至多\(k\)个顶点的子图,并且\(G\)中的每条边都至少有一个端点在这个子图中。
NPC证明¶
假设我们现在已经知道Clique problem是一个NPC问题,我们来证明Vertex cover problem也是一个NPC问题。
Proof
首先,检查一个解\(V^{'}\)的顶点数。然后,对于每一条边(u,v),检查是否满足\(u \in V^{'} \text{or } v \in V^{'}\).时间复杂度为\(O(N^2)\)
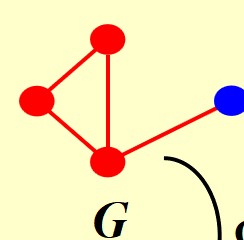
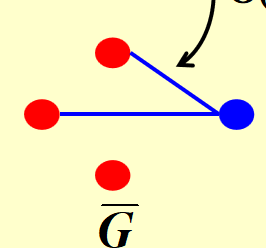
考虑这样的\(G\)与\(\bar G\)
若\(\bar G\)有size为\(\left| V \right| - K\)的点覆盖,则G有size为K的clique
若 \(G\) 有一个大小为 \(K\) 的团 \(V' \subseteq V\),设 \((u, v)\) 为 \(\bar E\) 中的任意一条边(E是G中边的集合,\(\bar E\)就是完全图减去原来有的边的集合,也就是\(\bar G\)中边的集合)。
则:
-
至少 \(u\) 或 \(v\) 中的一个不属于 \(V'\)
-
至少 \(u\) 或 \(v\) 中的一个属于 \(V - V'\)
所以\(\bar G\) 的每一条边都被 \(V - V'\) 中的一个顶点覆盖
因此,集合 \(V - V'\),其大小为 \(|V| - K\),构成了 \(\bar G\) 的一个顶点覆盖。
若 \(\bar G\) 有一个大小为 \(|V| - K\) 的顶点覆盖 \(V' \subseteq V\)
对于所有 \(u, v \in V\),如果 \((u, v) \notin E\),则 \(u \in V'\) 或 \(v \in V'\) 或两者都属。
对于所有 \(u, v \in V\),如果 \(u \notin V'\) 且 \(v \notin V'\),则 \((u, v) \in E\)。
因此,\(V - V'\) 是一个团,并且它有大小 \(|V| - |V'| = K\)。
最后,由于G到\(\bar G\)的转变是\(O(N^2)\)复杂度的,所以我们有CLIQUE \(\leq_p\) VERTEX-COVER。
综上,我们证明了Vertex cover problem 也是NPC问题。
例题¶
例题