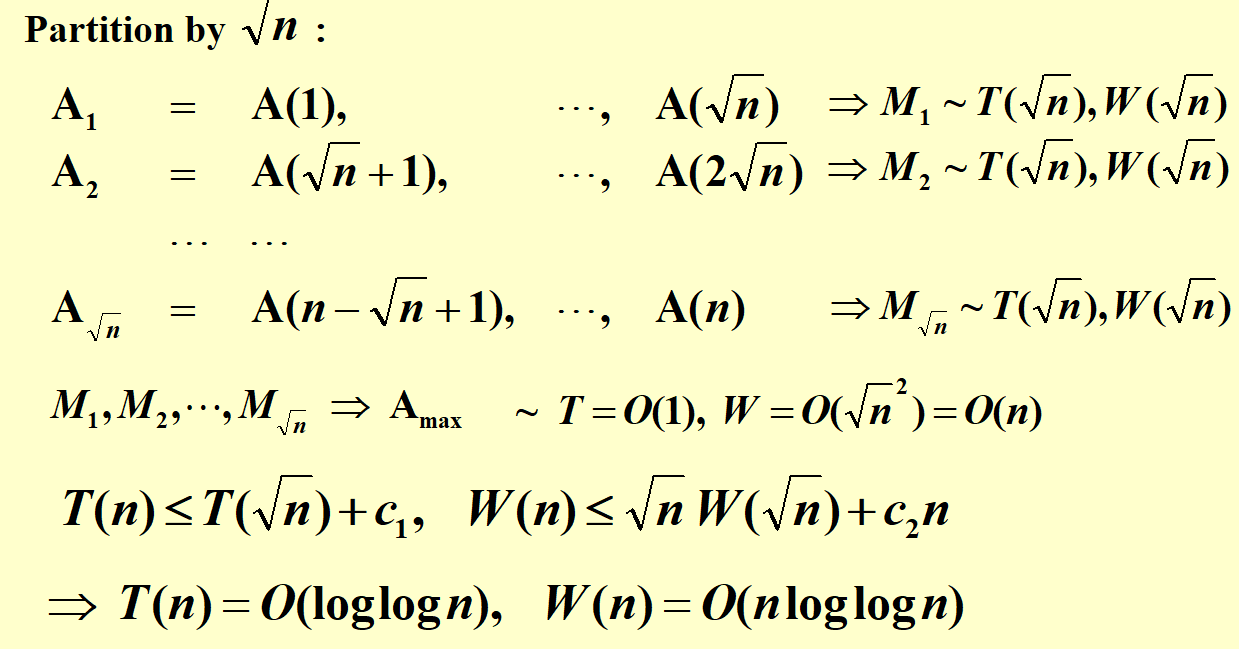Warning

这部分写得略混乱，可以移步Bruce的笔记

并发计算¶

约 2867 个字 44 行代码 18 张图片预计阅读时间 15 分钟

并发计算有两种类型:

指令集的并发(Machine parallelism)：处理器的多核心，流水线等
并发算法(Parallel algorithms)：多个线程同时执行

这里我们主要讨论并发算法。并发算法又有两种方式描述：

PRAM: 并行随机访问机器(Parallel Random Access Machine)
WD: 工作深度(Work Depth)

PRAM¶

假设我们有$P_1,P_2,\cdots,P_n$个处理器，所有的处理器共享一块内存。为方便讨论，我们认为读/写/计算都是花费一个单位时间的。

例如，如果我们想把B数组里的内容写到A数组里，在n个处理器的情况下只需要$O(1)$的时间，因为每个处理器只负责写一个元素。

但是，对于多个处理器同时访问内存，难免不会出现内存冲突的情况，为解决这些冲突，有如下方法:

Definition

EREW(Exclusive Read Exclusive Write): 任意两个处理器不能同时读写同一个地址
CREW(Concurrent Read Exclusive Write): 任意两个处理器可以同时读，但不能同时写
CRCW(Concurrent Read Concurrent Write): 任意两个处理器可以同时读写，但是仍可能发生写入冲突的情况，不同的解决方法有如下几种：
1. Common Rule:如果所有处理器写入的值相同，允许同时写入
2. Priority Rule:给处理器编号，编号小的优先写入
3. Arbitrary Rule:随机选择一个写入

The Summation Problem¶

最常见的问题，输入$A(1), A(2), \cdots, A(n)$,输出$A(1)+A(2)+\cdots+A(n)$

正常来说，这个问题的时间复杂度是$O(n)$，但是我们可以通过PRAM来优化。

考虑二维数组$B[i,j]$，代表了第i步的第j个处理器的值，那么一开始，我们可以在O(1)的时间内使用多个处理器将A数组的值写到B的第一行。

然后，我们可以在O(1)的时间内将B的每一行的值相加，最后得到结果。

于是我们得到:

\[B(h, i) = B(h-1, 2i-1) + B(h-1, 2i)\]

PRAM¶

from PPT

这里的pardo指的是并行执行，即多个处理器同时执行。

这样的时间复杂度是$O(\log n +2)$

PRAM的缺陷

该模型无法揭示算法和实际使用的处理器个数之间的关系
- 对于上面的例子，假如有 100 个处理器，但实际上只用了 8 个处理器，所以更多的处理器并不能使执行速度进一步加快
该模型需要指定哪个处理器处理哪部分的指令，这些详细信息其实是非并行算法所不需要的

WD¶

为此，我们引入了WD的概念，即工作深度。

性能的度量¶

传统算法从时间复杂度来度量性能，但是并发算法不同，因为并发算法的时间复杂度和处理器数量有关。处理器多了，跑得当然快了，但与此同时，工作量也增加了。

因此，我们使用时间复杂度与工作复杂度(Work Load)两个值来衡量。

我们的目标是，既要马儿跑得快，又要马儿吃得少。

T(n)与W(n)

$T(n)$: 干活最多的那个处理器，干的时间
$W(n)$: 所有处理器工作量总和

借用上面的例子说明

在求和问题中，WD性能为:

\[T(n) = \log n +2\]

这个看上面的图就可以理解，有一个处理器是在树的每一层都要干活的，加上一开始读取数据和最后的输出，所以是$\log n +2$

\[\begin{align} W(n) = n +n/2 + \cdots + n/2^k(2^k=n) +1= 2n \end{align}\]

这里是因为，在树的最底层，n个处理器都干活了，所以是n，然后上一层是n/2，一直到树的顶层，只有一个处理器在干活，所以是1。

其实还有最开始的读取和最后的输出，分别需要n和1的工作量，不过不影响最后工作量的量级。

对于PRAM来说:

当使用处理器数量$P(n) =\frac{W(n)}{T(n)}$时，操作的最差时间复杂度是$O(T(n))$
当使用处理器数量$P(n) \leq \frac{W(n)}{T(n)}$时，操作的最差时间复杂度是$\frac{W(n)}{P(n)}$(也就是处理器不足的情况)
对于任意数量的P(n)，操作的最差时间复杂度是$\frac{W(n)}{P(n)} + T(n)$

实际上，这三种评估方式是渐进等价(Asymptotically Equivalent)，也即，当n趋近于无穷大时，这三种评估方式是同一复杂度。

而对于WD来说，有以下定理:

WD-presentation Sufficiency Theorem

一个 WD 模式下的算法可以由任意 P(n) 个处理器在 O(W(n)/P(n) + T(n)) 时间内实现，使用并发写入。

Prefix-Sums¶

Prefix-Sums问题是这样的，给定一个数组$A(1), A(2), \cdots, A(n)$，求$B(1), B(2), \cdots, B(n)$，其中$B(i) = A(1)+A(2)+\cdots+A(i)$

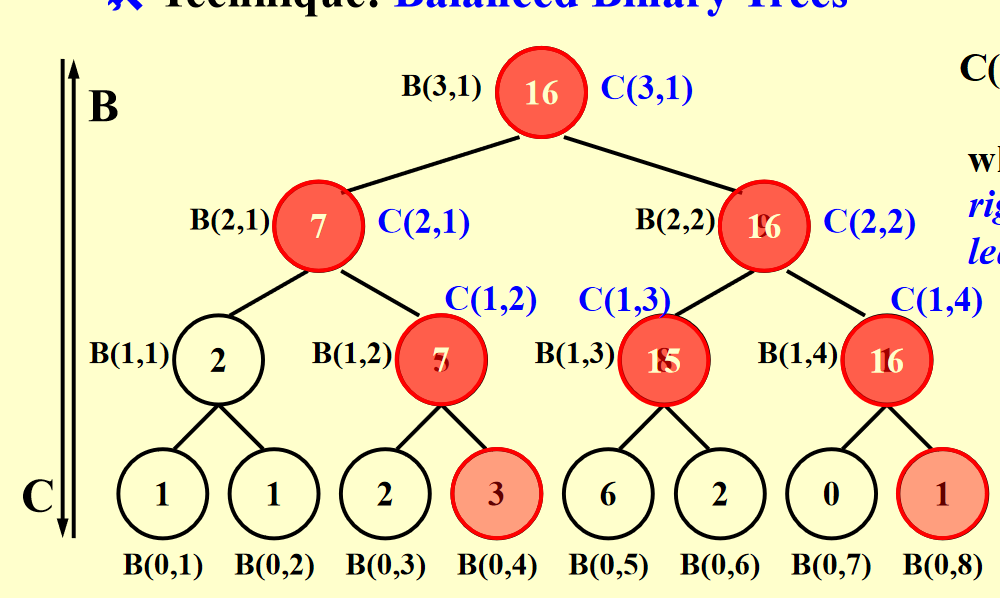
首先，建立如下的平衡二叉树:

可以看到，这里还是先计算了求和问题，为之后前缀和问题的解决打下基础。

然后，我们定义:

\[C(h,i)= \sum_{k=1}^\alpha A(k)\]

其中$\alpha$是(h,i)这个节点最右边的叶子节点的编号。

于是就有这样一张图:

我们可看出:

当i为1时:

if(i==1)
    C(h,i) = B(h,i)

当i为偶数时:

else if(i%2==0)
    C(h,i) = C(h+1,i/2)

当i为奇数时:

else
    C(h,i) = C(h+1,(i-1)/2) + B(h,i)

因此，我们先自底向上计算求和问题，然后根据求和问题的结果自顶向下计算前缀和问题

Prefix-Sums

for Pi , 1 <= i <= n pardo
  B(0, i) := A(i)
for h = 1 to log n
  for i , 1 <= i <= n/2^h pardo
    B(h, i) := B(h - 1, 2i - 1) + B(h - 1, 2i)
for h = log n to 0
  for i even, 1 <= i <= n/2^h pardo
    C(h, i) := C(h + 1, i/2)
  for i = 1 pardo
    C(h, 1) := B(h, 1)
  for i odd, 3 <= i <= n/2^h pardo
    C(h, i) := C(h + 1, (i - 1)/2) + B(h, i)
for Pi , 1 <= i <= n pardo
  Output C(0, i)

这样的做法下,$T(n) = O(\log n)$,$W(n) = O(n)$

这是很显然的，可以看作是求和问题的两倍，因为自底向上算$B(h,i)$的时候是一遍，自顶向下算$C(h,i)$的时候又是一遍。

Tip

如果要求前缀最大值(最小值)，只需要把求和问题的"+"换成"max"(或"min")即可,T(n)与W(n)不变。

Merging¶

Merging问题是这样的，给定两个已经排好序(升序)的数组$A(1), A(2), \cdots, A(n)$和$B(1), B(2), \cdots, B(n)$，求合并后的数组$C(1), C(2), \cdots, C(2n)$

我们约定:

A,B内元素两两不相等
$n = m$
$\log n ,\frac{n}{\log n}$都是整数

分割样例

分割 - 将输入划分为大量的、彼此独立的小任务，例如 p 个，使得最大的一个小任务的大小大致为 n/p
实际工作 - 并发地执行这些小任务，每个任务使用一个独立的（可能是串行的）算法

在这里，我们核心的目标是找到原来的元素在合并后的数组中的位置。

设想，对于一个B数组中的元素，我们只需要知道A,B中一共有几个元素比它小，就可以知道它在合并后的数组中的位置。

B中比这个元素小的个数很简单，就是它的编号，而在A中我们需要去找有几个元素比它小。

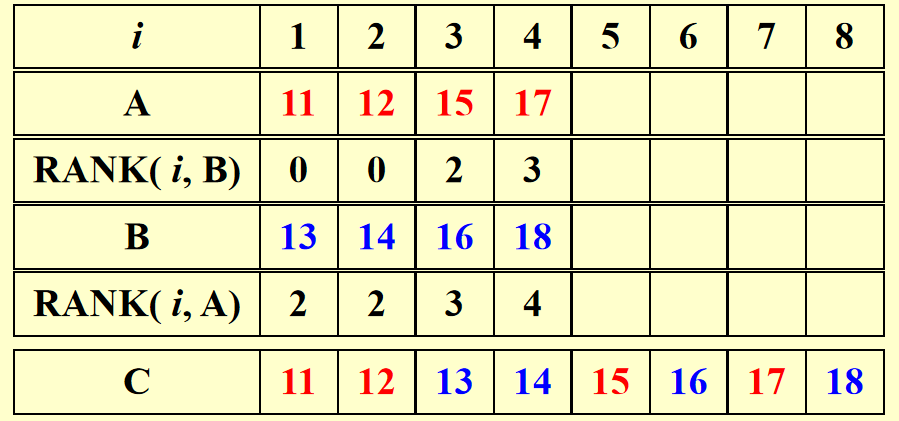
因此我们定义一个RANK函数如下，用于寻找B中第j个元素在A中能排第几:

$RANK( j, A) = i, if A(i) < B(j) < A(i + 1), 1 \leq i < n$
$RANK( j, A) = 0, if B(j) < A(1) $
$RANK( j, A) = n, if B(j) > A(n)$

因此总的任务就是跑完RANK(j,A)与RANK(i,B)。

如果我们得到了所有RANK的值，那么我们就可以在O(1)的时间内得到合并后的数组。因为有这样的并发算法使用n个处理器:

for Pi , 1 <= i <= n  pardo
    C(i + RANK(i, B)) := A(i)
for Pi , 1 <= i <= n(也即是m) pardo
    C(i + RANK(i, A)) := B(i)

结果示例:

Question

那么我们要如何计算RANK的值呢？

我们先来看两个朴素的算法:

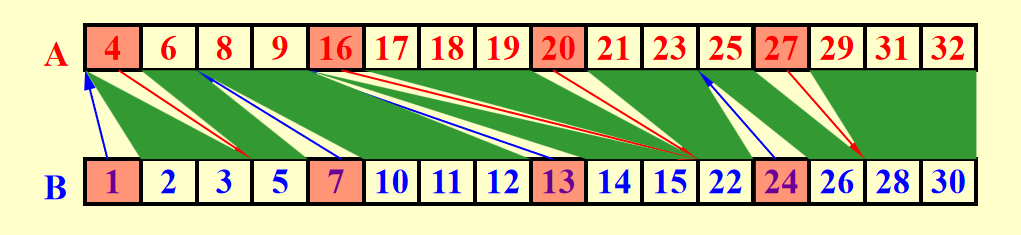
朴素算法

Serial RankingBinary Search

i = j = 0; 
while ( i <= n || j <= m ) {
    if ( A(i+1) < B(j+1) )
        RANK(++i, B) = j;
    else RANK(++j, A) = i;
}

此时，$T(n) = O(n+m)$,$W(n) = O(n+m)$

for Pi , 1 <= i <= n  pardo
    RANK(i, B) := BS(A(i), B)
    RANK(i, A) := BS(B(i), A)

此时，时间复杂度为$O(\log n)$是很小的，而且由于我们可以并行处理，因此总的时间复杂度也是$O(\log n)$

但是这样的工作量是很大的。每一个处理器都干了$2\log n$的活，这样的话，总的工作量就是$O(n\log n)$。

因此，我们把原来的数据分割为$p=\frac{n}{\log n}$块，每块的头一个元素寻找RANK值，形成了图中的箭头。这里相当于是p个二分查找并行，因为我们要为p个元素找到RANK值，因此$T(n) = O(\log n)$，$W(n) = p \log n = O(n)$

箭头划分出至多2p个区域。每一块区域并行处理，区域内部使用朴素的串行算法。

这样每块的大小为$\log n$，总的工作量为$p \log n = O(n)$，时间复杂度为$O(\log n)$

综上，我们得到了一个时间复杂度为$O(\log n)$，工作量为$O(n)$的算法。

Maximum Finding¶

Maximum Finding问题是这样的，给定一个数组$A(1), A(2), \cdots, A(n)$，求最大的元素。

朴素的想法¶

如果要求前缀最大值(最小值)，只需要把求和问题的"+"换成"max"(或"min")即可,T(n)与W(n)不变。

Compare all pairs¶

另给出一种算法:

Compare all pairs

for Pi , 1 <= i <= n  pardo
    B(i) := 0
for i and j, 1 <= i, j <= n  pardo
    if ( (A(i) < A(j)) || ((A(i) = A(j)) && (i < j)) )
        B(i) = 1
    else B(j) = 1

for Pi , 1 <= i <= n  pardo
    if B(i) == 0
       A(i) is a maximum in A

这种算法跑一遍，$T(n) = O(1)$，$W(n) = O(n^2)$

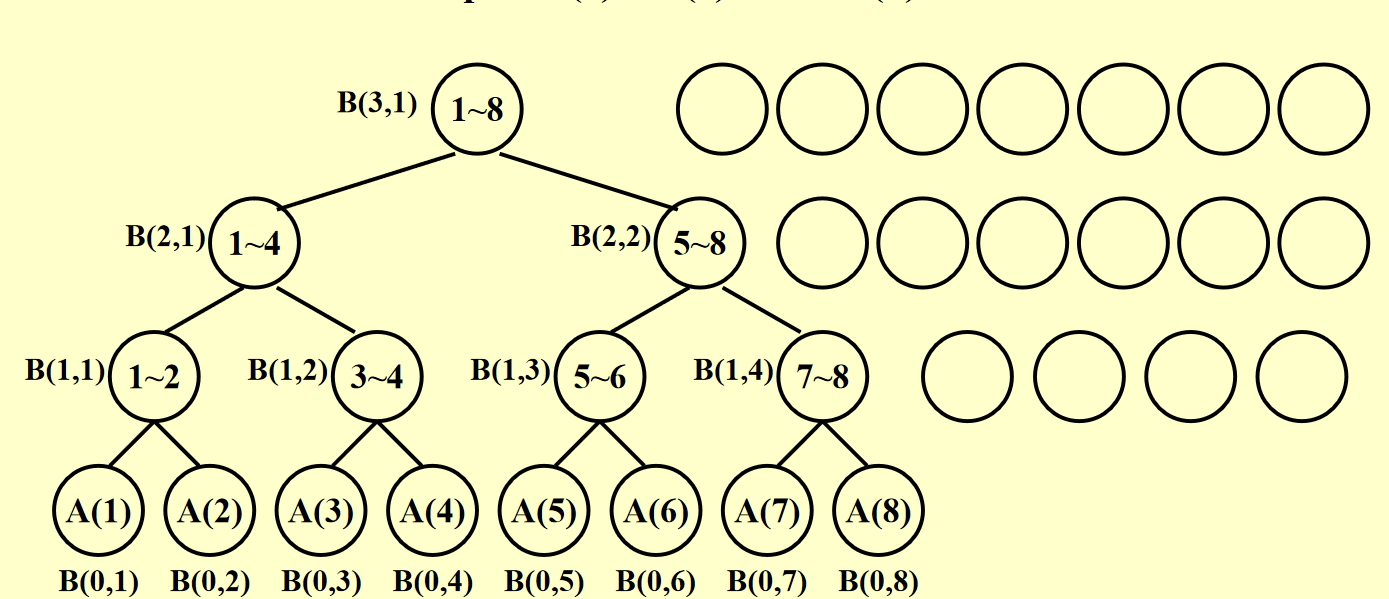
分割¶

如果我们以$\sqrt{n}$分割，每块内部用普通的串行算法寻找最大值，合并时用上面的算法寻找最大值，结果如下：

还有一种分割方法如下:

Random Sampling¶

~~没想到吧，还有一种做法~~

把数组A中随机挑$n^{\frac{7}{8}}$个元素出来，形成数组B
将数组B划分为$n^{\frac{3}{4}}$个大小为$n^{\frac{1}{8}}$的小块,小块内部使用Compare all pairs算法求出最大值，得到$n^{\frac{3}{4}}$个最大值,$T(n) = O(1),W(n) = n^{\frac{3}{4}} * (n^{\frac{1}{8}})^2 = O(n)$
接下来将这些最大值划分为 $n^{\frac{1}{2}}$ 个大小为 $n^{\frac{1}{4}}$ 的小块，然后对每个小块求出最大值，得到$n^{\frac{1}{2}}$个最大值.（使用 Compare All Pairs 方法计算）$T(n) = O(1),W(n) = n^{\frac{1}{2}} * (n^{\frac{1}{4}})^2 = O(n)$
再使用$n^{\frac{1}{2}}$个最大值求出所有 $n^{\frac{7}{8}}$ 个元素的最大值（使用 Compare All Pairs 方法计算）$T(n) = O(1),W(n) = (n^{\frac{1}{2}})^2 = O(n)$

总的来说，时间复杂度是$O(1)$，工作量是$O(n)$。但是这个算法不能保证找到最大值，只能说有很大的概率找到最大值。

例题¶

例题

T1T2T3T4T5T6T7T8T9

解析

F.还需要考虑T(n)的值

解析

T.C是自顶向下算的。

解析

T.B是自底向上算的。

解析

F。采用 Random Sampling，就可以在O(n)的开销下。

解析

T.见定义

解析

C.这其实就是把Summation问题的"+"换成了"min"

解析

D.见定义。

解析

A.按我的理解，递归深度有$\log n$层，使用Parallel Ranking可以让每层的$W(n)=O(n)$，综合起来的工作量是$O(n\log n)$。而对于$T(n)$,最底下那层是$\log 1$，往上一层是$\log 2$,以此类推是$\log 4,\log 8,\cdots,\log n$，不妨设$n=2^l$,那么

$T(n)=\log 1 + \log 2 + \cdots + \log n =(0 + 1 + \cdots +l) \log 2 = \frac{l(l+1)}{2}\log 2 = O(\log^2 n)$

解析

D.见Parallel Ranking。

并发计算¶

PRAM¶

The Summation Problem¶

PRAM¶

WD¶

性能的度量¶

Prefix-Sums¶

Merging¶

Maximum Finding¶

朴素的想法¶

Compare all pairs¶

分割¶

Random Sampling¶

例题¶

评论