Arithmetic for Computer¶
约 976 个字 23 张图片 预计阅读时间 5 分钟
Arithmetic¶
加法¶
不管什么表示，直接加就是对的（包括负数的补码表示）。
加法
减法¶
减去一个数等于加上这个数的补码。
减法
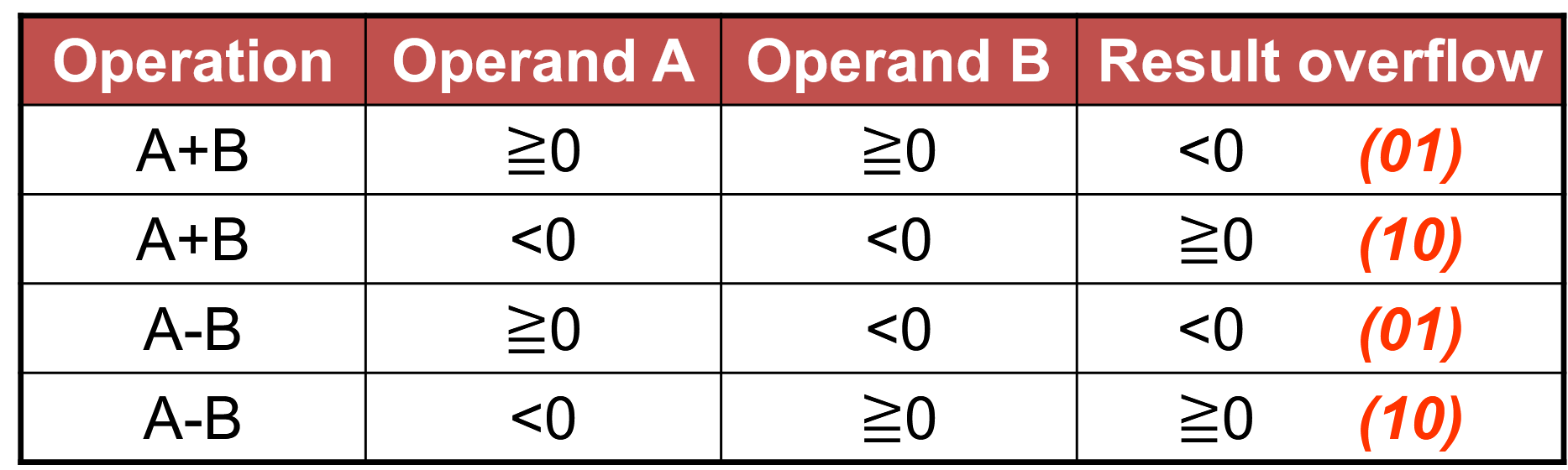
Overflow¶
定义次高位向最高位的进位为\(c_i\),最高位的进位为\(c_{i+1}\),则溢出检验可定义为\(c_i \oplus c_{i+1}\),若结果为1则发生溢出。
溢出情况
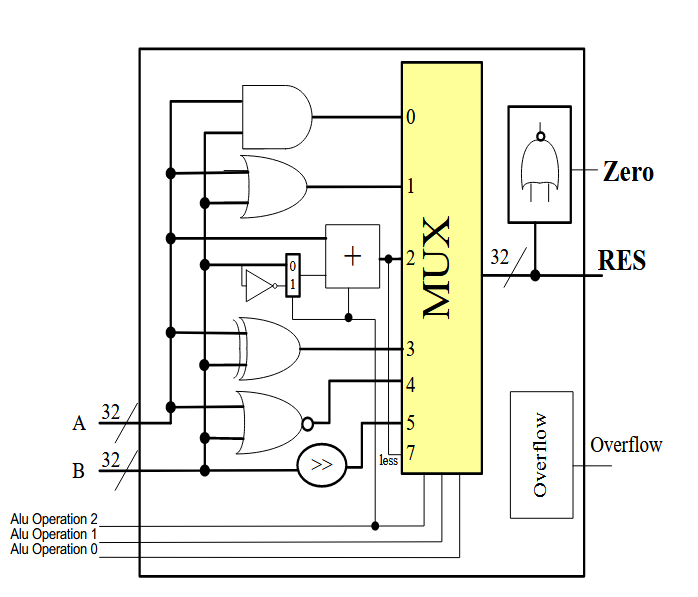
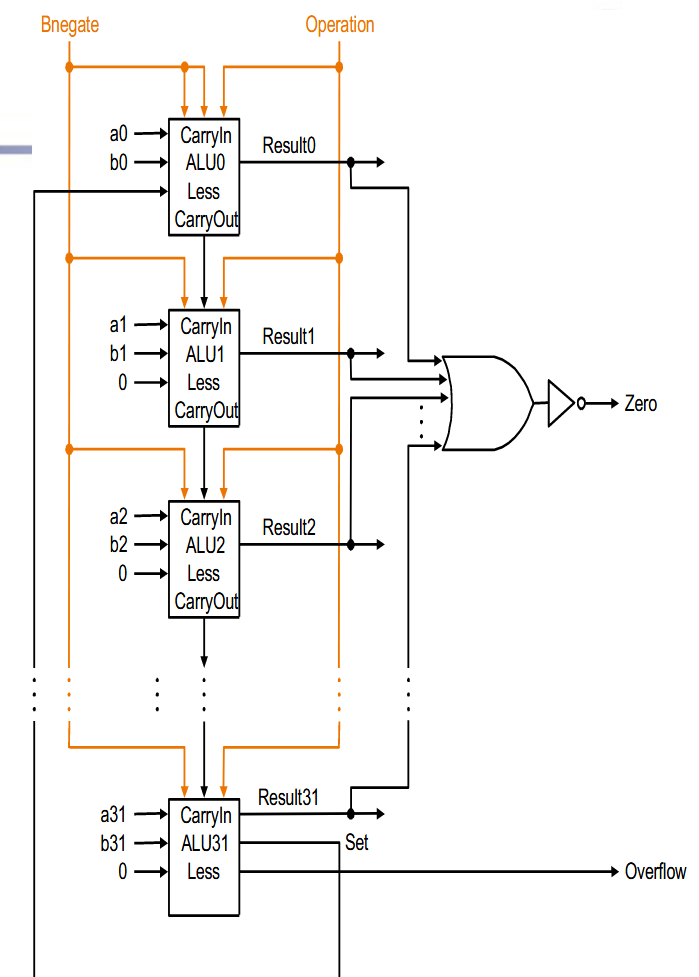
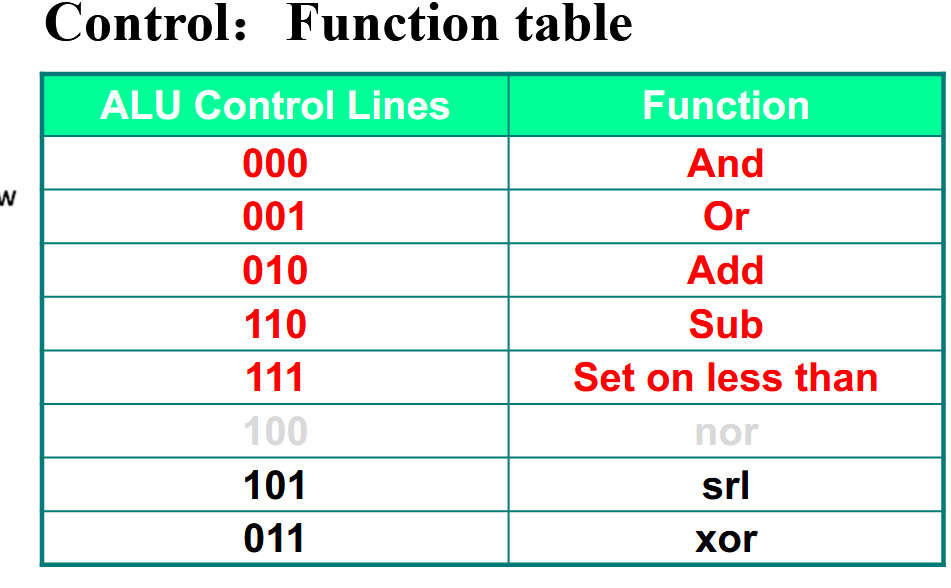
ALU¶
在数字逻辑中已经设计过
ALU
说明
- slt:比较大小
- srl:移位
- 目前还不支持非或
乘法¶
朴素的思路¶
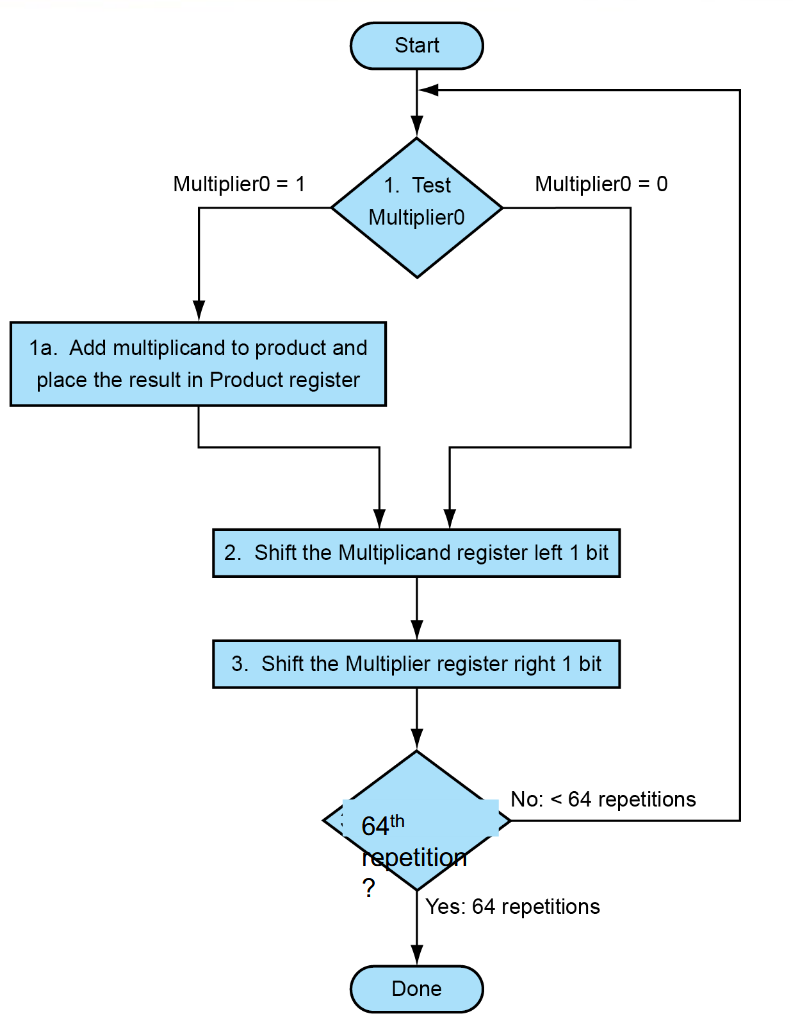但是这样会很慢，因此有一种优化的思路，可以将ALU的位数降下来。
改进V2¶
V2
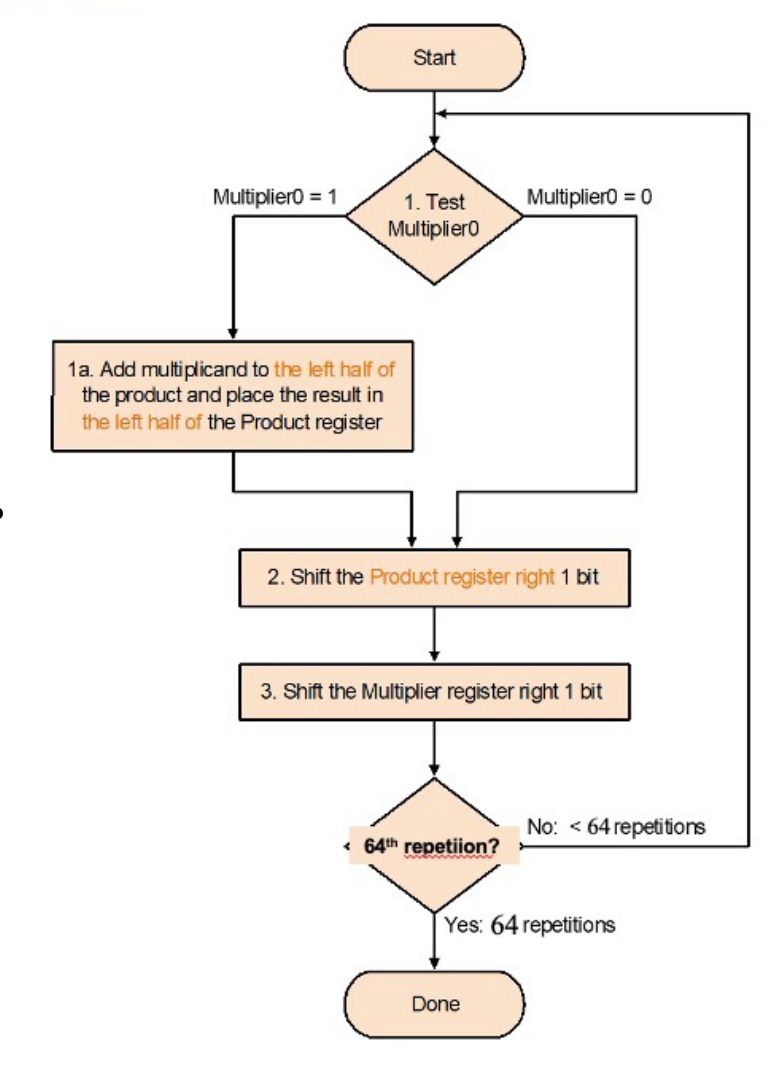
这时我们又想到，乘法运算的结果和乘数每次都要右移一位，结果是乘数丢弃一位，product要增加一位。那我们能不能让增加的这一位利用丢弃导致空出来的位置呢？
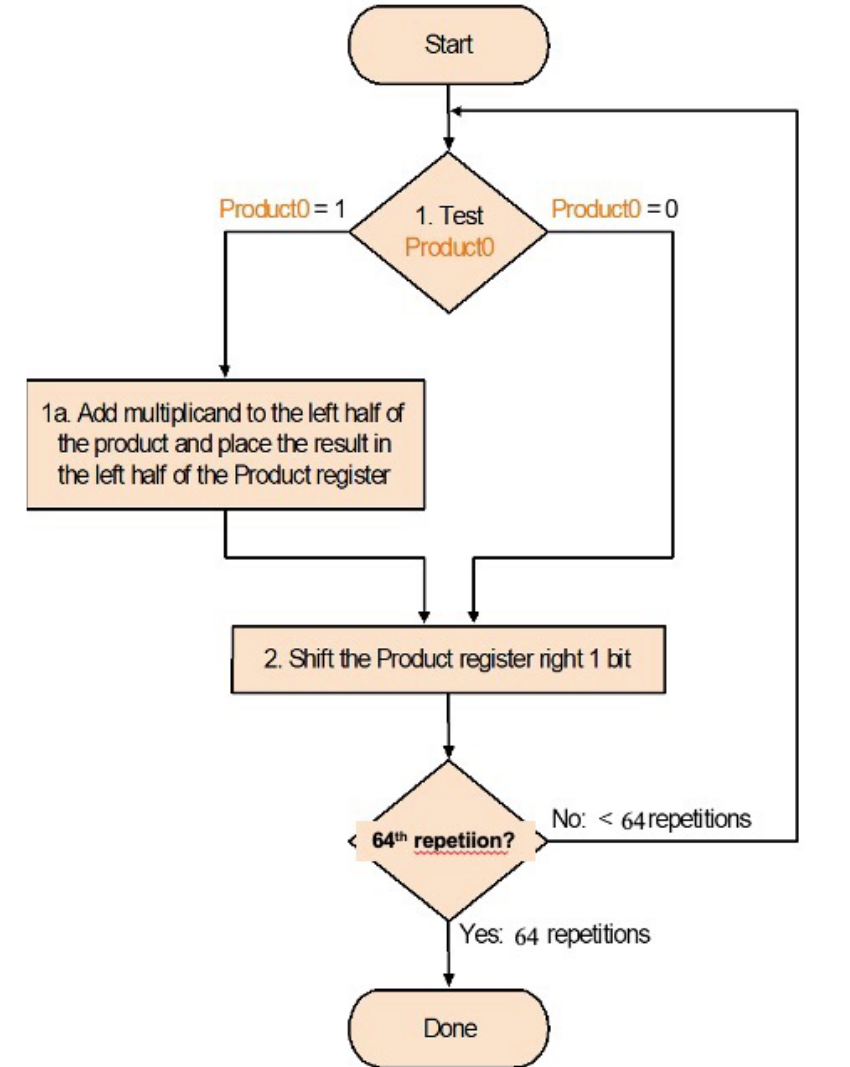
改进V3¶
V3
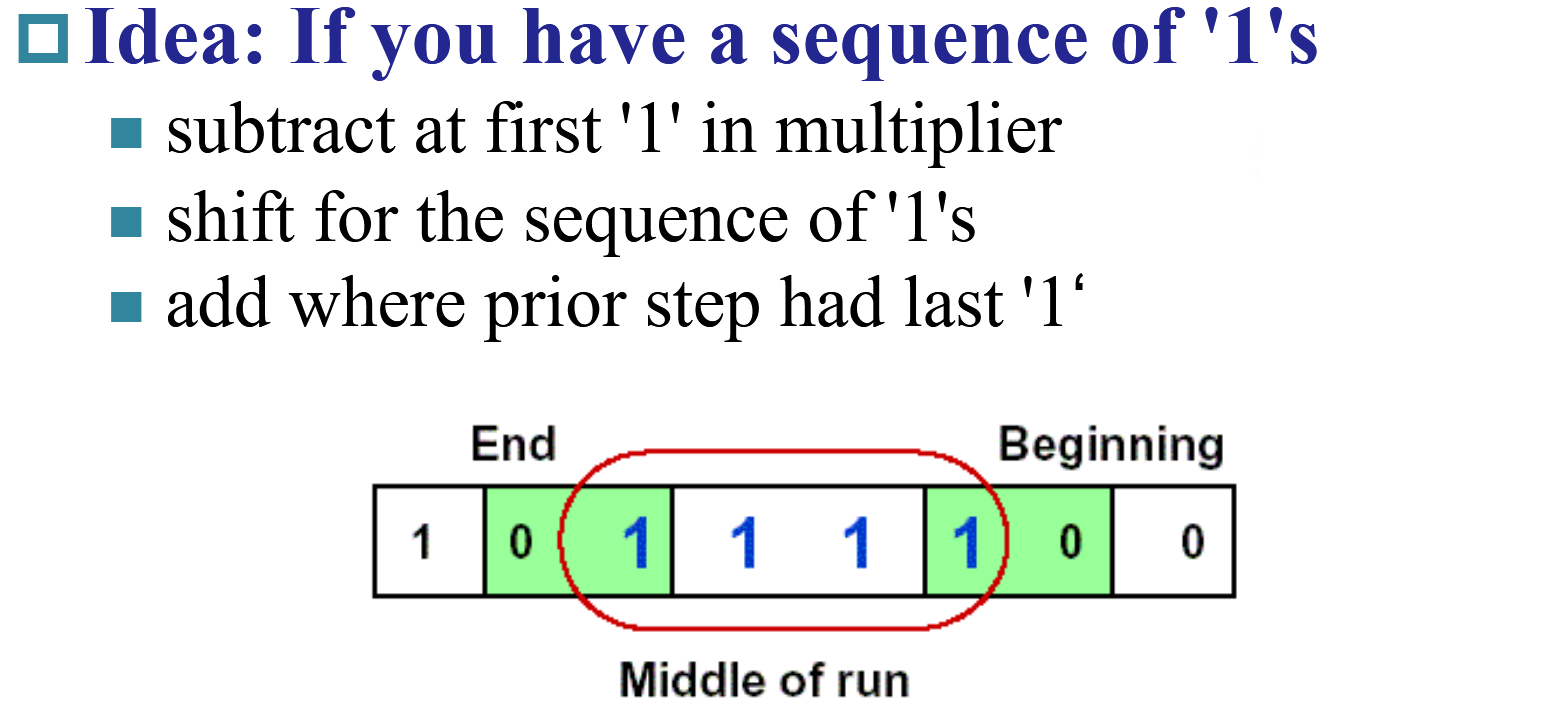
Booth¶
然后又有一个神人想出了一个神奇的方法，可以在乘数含大量1的情况下大大加快速度，思想类似于乘法分配律。
Booth
除法¶
思路¶
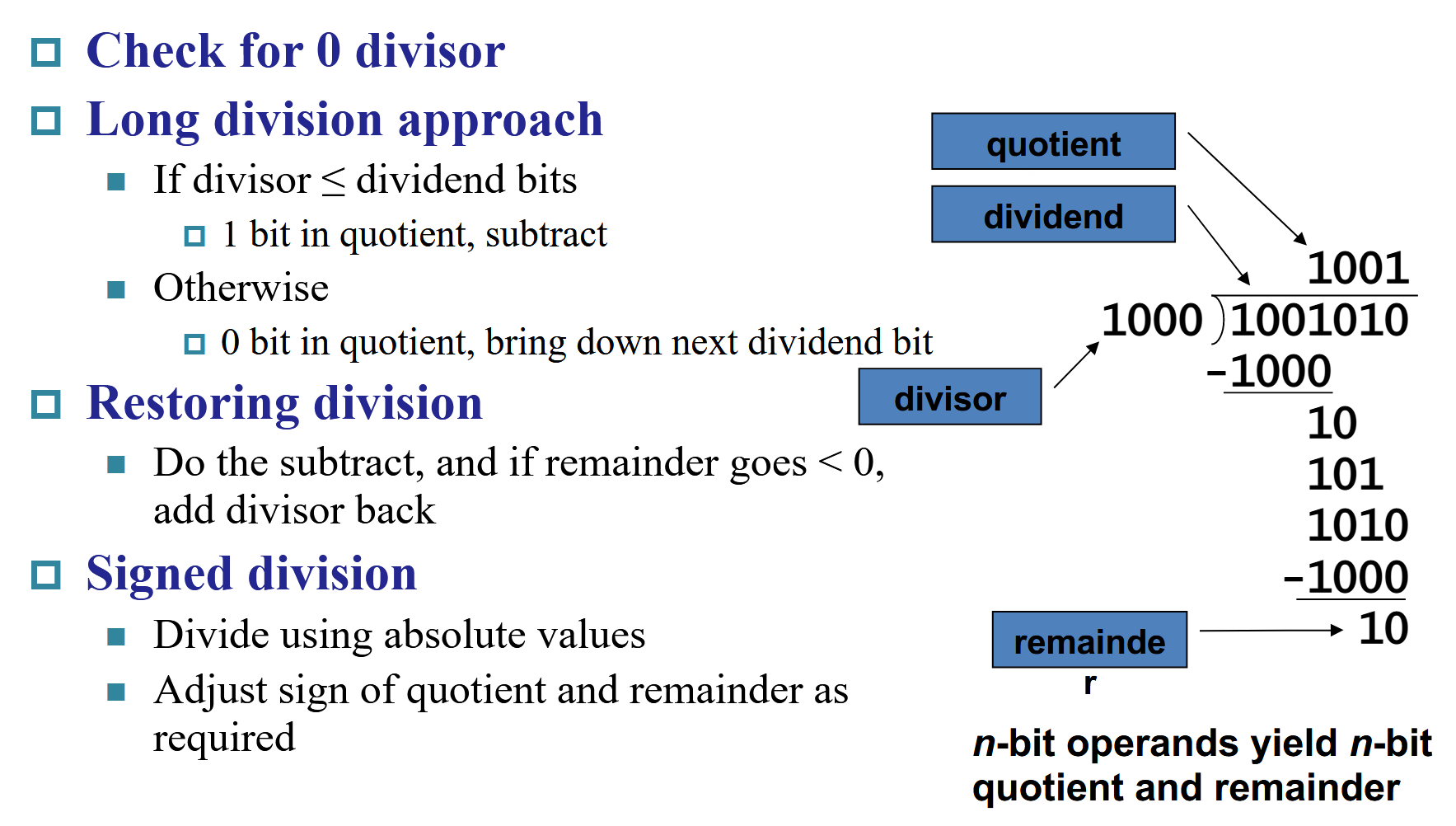
和小学学除法一样，用一个竖式来计算。
竖式运算
V1¶
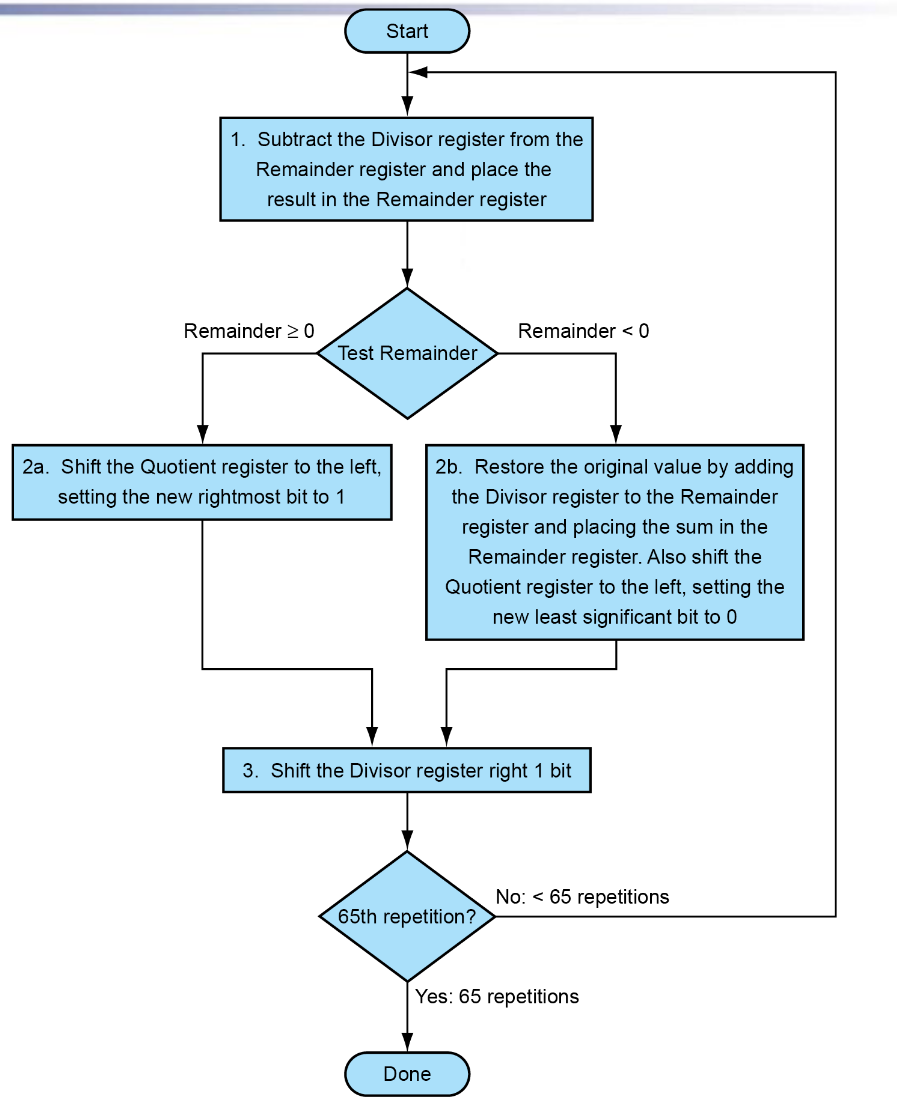
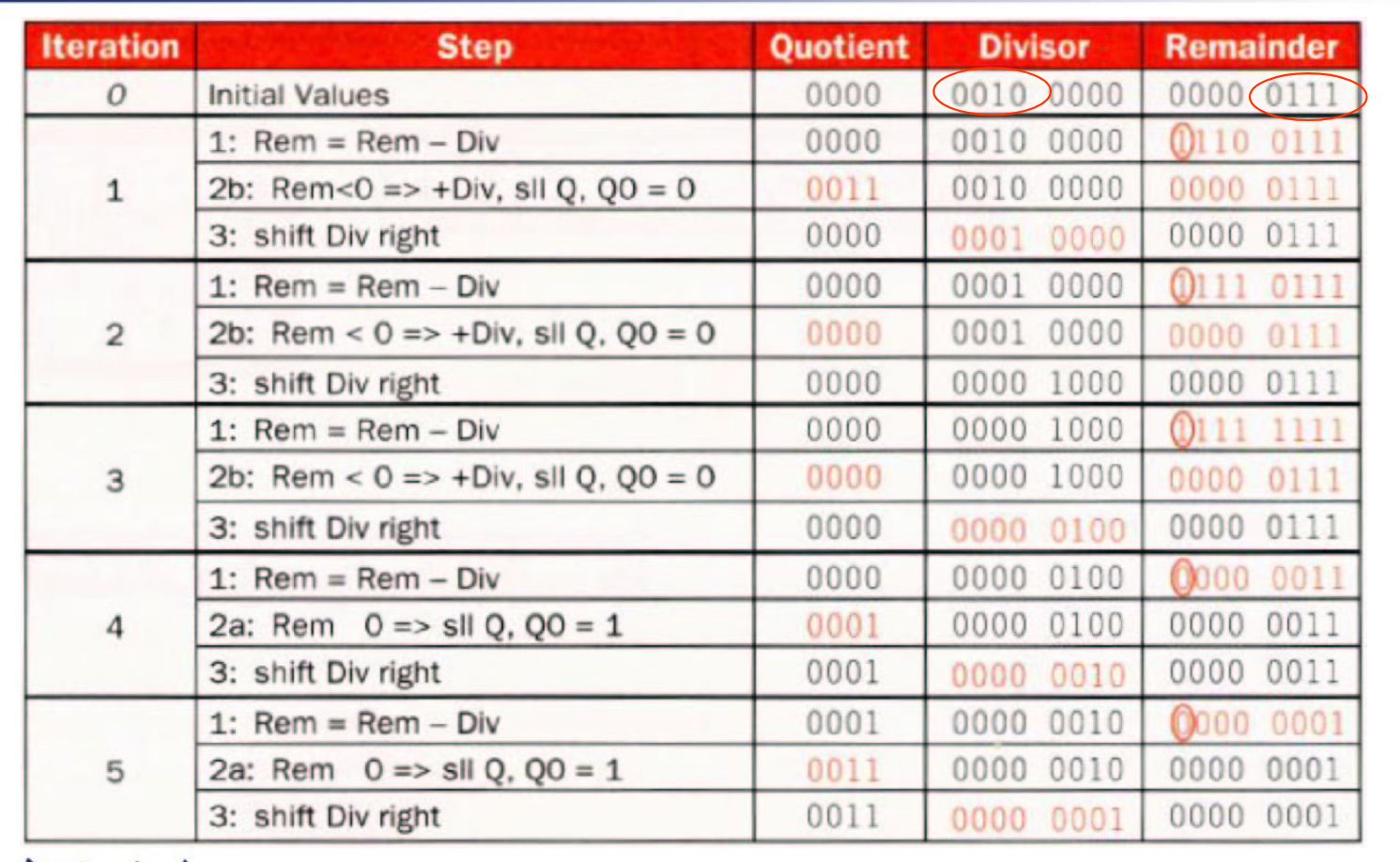
解析
-
把除数(divisor)放在左半部分，被除数(dividend)放在右半边，置于寄存器中。
-
把被除数减去除数，得到结果：
-
若结果大于0，商(Quotient)左移一位，最低位置为1
-
若结果小于0，把结果加上除数恢复原来的被除数，商左移一位，最低为置为0
-
-
除数右移一位
例子
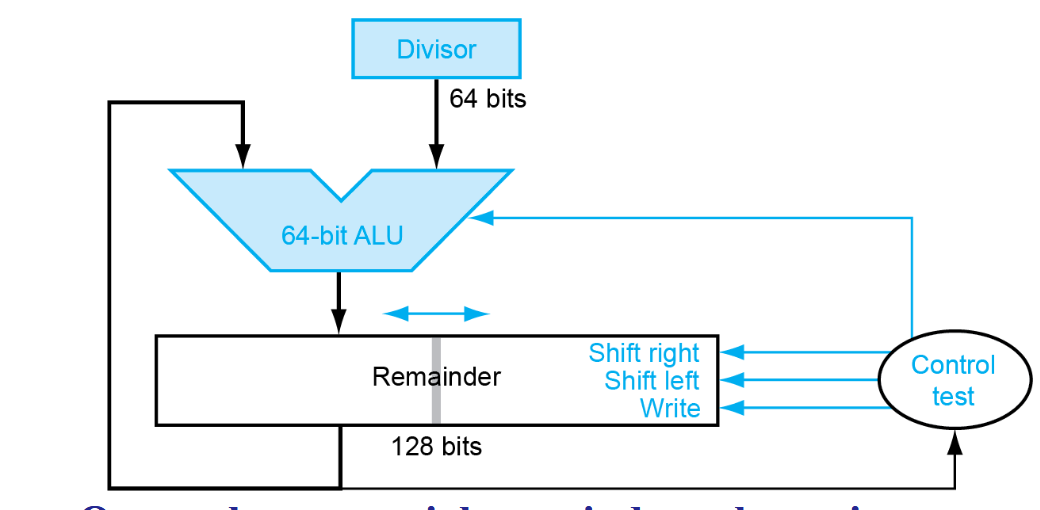
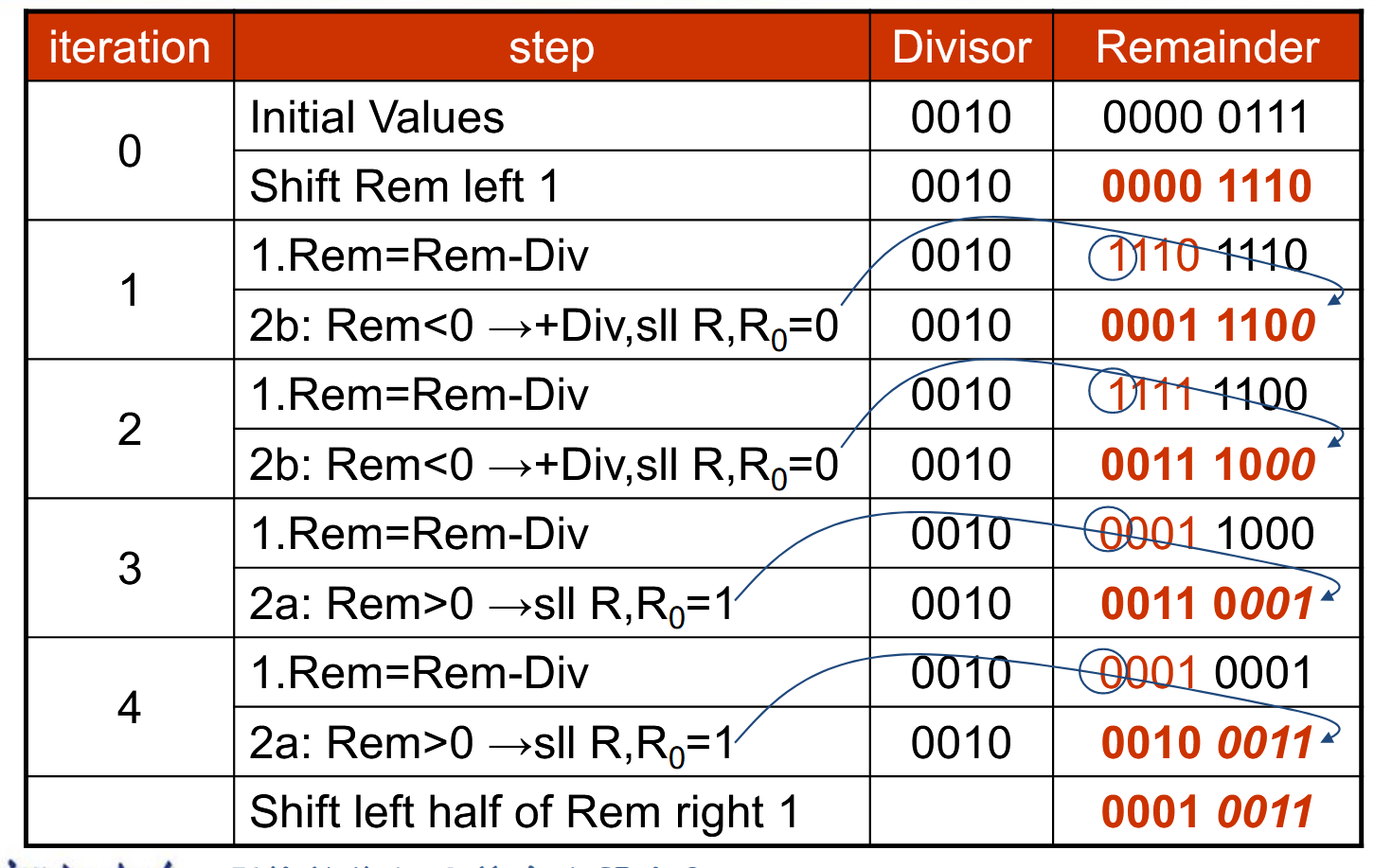
修改版本¶
上面的ALU是128位的，太过于浪费空间，有没有优化呢？ 我们考虑一个reminder，一开始被除数放在最右边，这样就分成了左边64位与右边64位。左边64位与除数作减法运算。每次被除数左移一位，计算减法结果，根据是否大于0在左移空出来的最低位置1或0.
图例
这里的shift right有什么用呢
考虑乘法的硬件图，加上右移功能可以使这个结构可以同时处理乘法与除法
浮点数与运算¶
想象二进制的科学计数法，浮点数形如\(1.xxxxx \times 2^{yyyyy}\)
在表示时，1可以直接省去，因为肯定是1
精度(precision)¶
有单精度(Single precision)与双精度(Double precision)两种
组成
result=\(-1^{\text{sign}} \times (1+significand) \times 2^{exponent - bias}\)
1位符号位，8位指数位，23位小数位组成。指数bias=127
示例：-0.75
解析
-0.75在二进制下为\(-1.1 \times 2^{-1}\)
因此符号位是1，指数位是\(-1+127=126\),小数位是1....0
在单精度的基础上多了一个字的大小存小数，因此叫双精度。bias=1023
示例：-0.75
解析
-0.75在二进制下为\(-1.1 \times 2^{-1}\)
因此符号位是1，指数位是\(-1+1023=1022\),小数位是1....0
加法¶
加法的步骤为
-
指数对齐，一般是小的指数往大的指数对齐。
-
做运算
-
归一化
-
检查溢出
-
round
-
选择性归一化
例子
乘法¶
小数相乘，指数相加，需要注意的是指数相加的结果需要减去一个bias，不然bias会加两次。
精确计算¶
IEEE Std 754建议了一些额外的位数，用来增加计算的精度。
-
Guard: The first of two extra bits.
-
Round: method to make the immediate floatingpoint result fit the floating-point format.
-
Units in the last place(ulp):The number of bits in error in the least significant bits of the significant between the actual number and the number that can be represented.