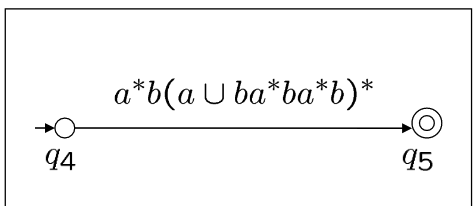自动机(Automata)¶

约 5016 个字 18 张图片预计阅读时间 25 分钟

自动机和数逻里面学过的有限状态机很相似,都有状态,输入,转换等概念.自动机是计算理论的基础,是形式语言的识别器.

面试

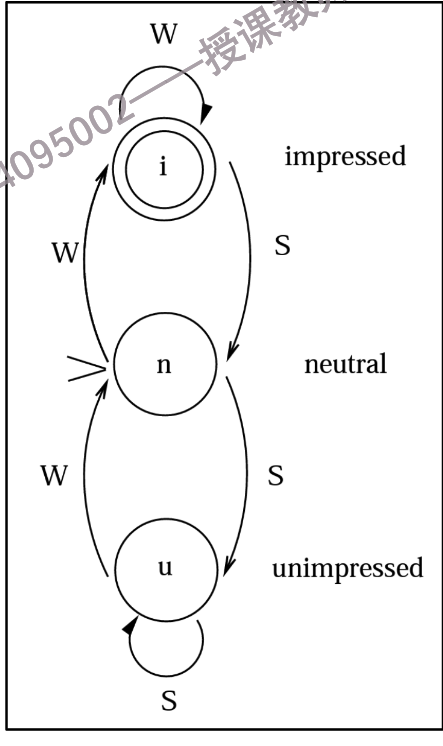
面试官有三种状态：印象深刻(impressed)、中立(neutral)和印象不佳(disappointed)。

初始时，面试官处于中立状态。
如果学生说了机智(witty)的话，面试官的印象会变好。
如果学生说了愚蠢(stupid)的话，面试官的印象会变差。

面试

DFA(Deterministic Finite Automata)¶

在决定有限自动机的图中,不同的状态有不同的符号:

Initial state(初始状态):有一个箭头指向它,表示自动机的开始状态.
State(状态):$ q_0, q_1, q_2 $ ,状态用圆圈表示.
Final state(终止状态):,双圈表示终止状态.到达终止状态即被接受.

而状态转移函数可以表达为:

\[ \delta:(q,a) = p \]

意思是:在状态q下,输入a,自动机转换到状态p.

图中q0既是初始状态也是终止状态

自动机(DFA)的定义

自动机是一个五元组$(Q, \Sigma, \delta, q_0, F)$,其中:

$Q$ 是有限状态集.
$\Sigma$ 是有限输入符号集(字母表).
$\delta$ 是状态转移函数,形式为 $\delta: Q \times \Sigma \rightarrow Q$.
$q_0 \in Q$ 是初始状态.
$F \subseteq Q$ 是终止状态集,包含一个或多个终止状态.

之所以是确定性的,是因为对于每个状态和输入符号,状态转移函数都唯一地确定了下一个状态.

自动机的作用

有限自动机是一种识别装置，它有有限个内部状态。自动机接收输入（通常是一串符号），并根据目前已经读到的输入序列，判断这个序列是否属于某种语言。如果属于该语言，自动机就“接受”输入（回答“yes”）；如果不属于，则“拒绝”输入（回答“no”）。

换句话说，自动机就是用来判断一个字符串是否符合某种规则（语言）的工具。

如果一个输入字符串被自动机接受,那么这个字符串就属于该自动机所识别的语言.

Configuration(配置)

自动机在某一时刻的配置可以用二元组 $(q, x)$ 表示，其中：

$q \in Q$：当前状态
$x \in \Sigma^*$：剩余的输入字符串（后缀）

对于自动机 $M = (Q, \Sigma, \delta, q_0, F)$，如果当前配置为 $(q, x)$，表示自动机处于状态 $q$，还剩下输入 $x$。

M的两个配置之间的二元关系$\vdash_M$

如果 $\delta(q, a) = p$，那么我们说配置 $(q, ax)$ 直接产生（yields）配置 $(p, x)$，记作：

\[ (q, ax) \vdash_M (p, x) \]

这表示在状态 $q$ 下读取输入符号 $a$ 后，自动机转移到状态 $p$，并且剩余输入变为 $x$。

如果存在一系列配置 $(q_1, x_1), (q_2, x_2), \ldots, (q_n, x_n)$，使得：

\[ (q_1, x_1) \vdash_M (q_2, x_2) \vdash_M \ldots \vdash_M (q_n, x_n) \]

那么我们说配置 $(q_1, x_1)$ 产生（yields）配置 $(q_n, x_n)$，记作：

\[ (q_1, x_1) \vdash^*_M (q_n, x_n) \]

这表示从初始配置 $(q_1, x_1)$ 出发，通过一系列状态转移，最终达到配置 $(q_n, x_n)$。

注意: 这里的 $\vdash^*_M$ 是 $\vdash_M$ 的反复应用，可以是零次或多次。

因此,我们现在可以定义一个字符串被自动机接受的条件:

对于自动机 $M = (Q, \Sigma, \delta, q_0, F)$，如果存在一个终止状态 $q_f \in F$，使得：

\[ (q_0, w) \vdash^*_M (q_f, \epsilon) \]

那么我们说字符串 $w$ 被自动机 $M$ 接受。

这里，$(q_0, w)$ 是初始配置，表示自动机从初始状态 $q_0$ 开始，输入字符串为 $w$；$(q_f, \epsilon)$ 是终止配置，表示自动机最终到达终止状态 $q_f$，且没有剩余输入（$\epsilon$ 表示空字符串）。

换句话说，如果自动机从初始状态出发，经过一系列状态转移后，能够在读取完整个输入字符串后停在某个终止状态，那么这个输入字符串就被该自动机接受。

对于$\epsilon$是否被接受,需要看初始状态是否是终止状态.

NFA(Nondeterministic Finite Automata)¶

非确定性有限自动机和确定性有限自动机的区别在于,对于某个状态和输入符号,可能有多个下一个状态.

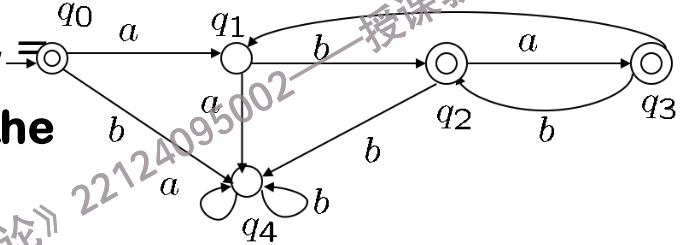
现在,我们希望实现一个自动机,判别一个字符串是否满足$(ab \cup aba)^*$,即字符串由"ab"和"aba"重复组成.

如果是决定性自动机,需要这样设计:

DFA for (ab ∪ aba)*

现在,我们希望通过非决定性自动机来实现,即允许一个状态和输入符号对应多个下一个状态.

定义¶

NFA和DFA的定义类似,五元组$(Q, \Sigma, \delta, q_0, F)$,其中:

$Q$ 是有限状态集.
$\Sigma$ 是有限输入符号集(字母表).
$\delta$ 是状态转移关系,是$Q \times (\Sigma \cup \{\epsilon\}) \times Q$的子集
- 这里的$\epsilon$表示空输入,即不需要输入符号也可以转换状态.
- 由于$\delta$的输出是一个状态集,所以,对于某个状态和输入符号,可能有多个下一个状态.
$q_0 \in Q$ 是初始状态.
$F \subseteq Q$ 是终止状态集,包含一个或多个终止状态.

除此之外,Configuration(配置)和接受条件与DFA一致.

NFA的图在绘制时,有几点不同于DFA:

状态转换箭头上可以标注$\epsilon$,表示不需要输入符号也可以转换状态.
对于某个状态和输入符号,可以有多个箭头指向不同的下一个状态.
不需要为一个状态的所有可能输入都定义转移,即可以不完整.如果在某个状态下，收到的输入符号没有对应的转移路径，那么这条计算“分支”就会“死亡”并被丢弃。

每一个NFA,都能被转换成一个等价的DFA

首先,我们必须了解什么是等价的NFA和DFA:如果一个NFA和一个DFA识别同一个语言,那么它们就是等价的.

其次,NFA与DFA的区别在于两点:

NFA的状态转换可以是非确定性的,即对于某个状态和输入符号,可能有多个下一个状态.
NFA允许$\epsilon$转换,即不需要输入符号也可以转换状态.

我们要做的就是抹平这两点差别.

消除第一点消除第二点

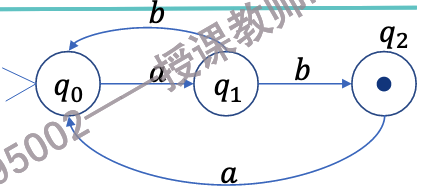
$M = (Q, \Sigma, \Delta, s, F)$

$Q = \{q_0, q_1, q_2\}$
$\Sigma = \{a, b\}$
$s = q_0$
$F = \{q_2\}$
$\Delta = \{ (q_0, a, q_1),\ (q_1, b, q_0),\ (q_1, b, q_2),\ (q_2, a, q_0) \}$

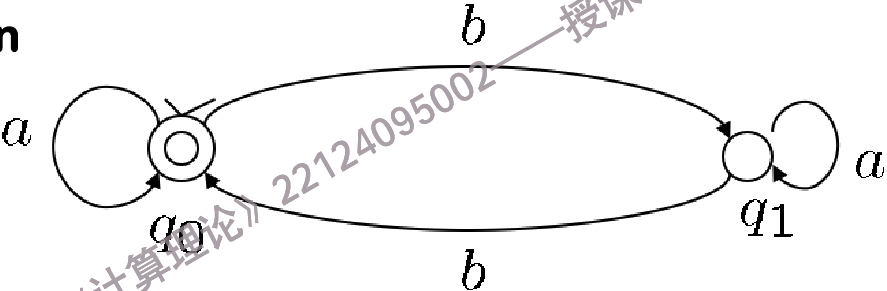
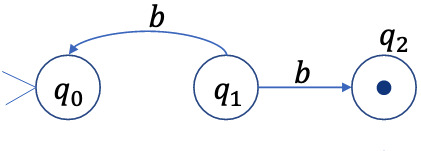
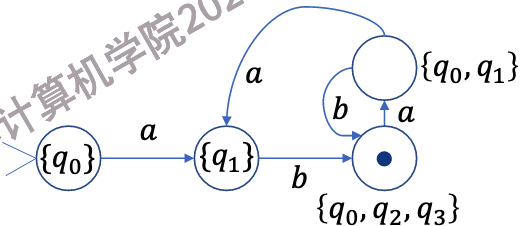
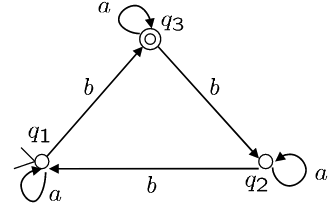
NFA的状态转换图如下:

NFA

其中,非确定性的部分在于:

非确定性

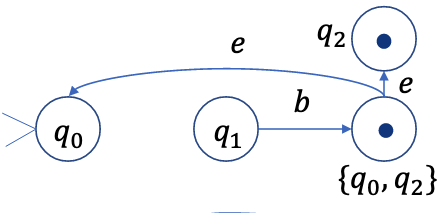
这里的非确定性来源于状态$q_1$在输入$b$时,可以转换到状态$q_0$或$q_2$.因此,我们把$q_0$和$q_2$合并成一个新状态$q_{0,2}$,表示可能处于状态$q_0$或$q_2$.这样,我们就消除了非确定性.

消除非确定性

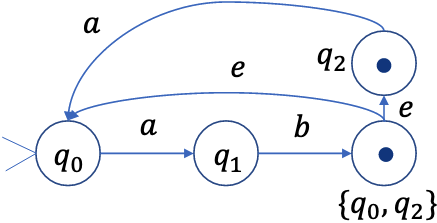
最后是这样:

最终结果

输入一个普通字符,可以看作是输入一个普通字符后面跟了许多空字符

基于这种思路,我们可以消除$\epsilon$转换.

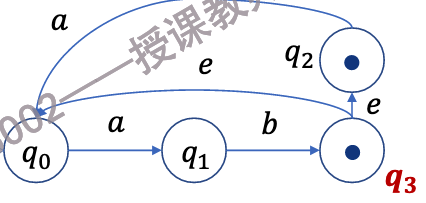
定义$E(q)$为从状态$q$出发,通过若干个$\epsilon$转换可以到达的所有状态的集合,包括$q$本身.

消除第一步的结果

实际上,对于$\epsilon$转换,我们应当把转换的两边状态看作是"等势"的,也就是说,它们面对后面输入的反应是一样的.

现在我们有

$E(q_0) = \{q_0\}$
$E(q_1) = \{q_1\}$
$E(q_2) = \{q_2\}$
$E(q_3) = \{q_0, q_2, q_3\}$

我们可以认为,$q_1$在输入$b$后,可以变为$E(q_3)$,即$\{q_0, q_2, q_3\}$

而$E(q_3)$在输入$a$后,可以变为$q_0,q_1$,因为它可以走$q_3 \rightarrow_{\epsilon} q_0 \rightarrow_a q_1$或$q_3 \rightarrow_{\epsilon} q_2 \rightarrow_a q_0$

因此,我们要做的就是把这些点合起来

消除第二步的结果

Make a DFA from an NFA

对于一个NFA $M = (Q, \Sigma, \Delta, s, F)$，我们可以构造一个等价的DFA $M' = (Q', \Sigma, \delta, s', F')$，其中：

$Q' = \mathcal{P}(Q)$：$Q$ 的幂集，表示所有可能的状态子集。
- 比如,在上面的例子中,$Q'$的状态出现了$\{q_0\}, \{q_1\}, \{q_2\}, \{q_0, q_2\}, \{q_0, q_3\}, \{q_2, q_3\}, \{q_0, q_2, q_3\}$等.
$\delta: Q' \times \Sigma \rightarrow Q'$：状态转移函数，定义为：对于$K \subseteq Q$和$a \in \Sigma$，有：

\[ \delta(K, a) = \bigcup_{q \in K} E(\{p \mid (q, a, p) \in \Delta\}) \]
- 也就是说,对于$K$中的每个状态$q$,找到所有$(q, a, p) \in \Delta$的$p$,然后计算这些$p$的$\epsilon$闭包,最后把这些闭包合并.
$s' = E(\{s\})$：初始状态是NFA初始状态的$\epsilon$闭包。
$F' = \{K \subseteq Q \mid K \cap F \neq \emptyset\}$：终止状态集包含所有与NFA终止状态有交集的状态子集。

Claim¶

对于任意字符串 $w \in \Sigma^*$ 和任意状态 $p, q \in Q$，有：

\[ (q, w) \vdash^*_M (p, \epsilon) \iff \exists P \ni p,\ (E(q), w) \vdash^*_{M'} (P, \epsilon) \]

其中，$E(q)$ 表示从状态 $q$ 出发通过若干 $\epsilon$ 转换可以到达的所有状态的集合（$\epsilon$-闭包），$M$ 是原NFA，$M'$ 是其等价DFA。

换句话说：

对于NFA $M$ 和其等价DFA $M'$，如果NFA能从状态 $q$ 经过输入 $w$ 到达状态 $p$ 并且输入耗尽，则DFA能从 $E(q)$ 经过 $w$ 到达某个包含 $p$ 的状态集合 $P$，且输入耗尽。

若上面这个Claim成立,那么我们就证明了NFA和DFA是等价的:

$ \forall w \in \Sigma^*,$

\[\begin{align*} w \in L(M) &\iff (s, w) \vdash^*_M (f, \epsilon) \text{ for some } f \in F \\ &\iff (E(s), w) \vdash^*_{M'} (Q, \epsilon) \text{ for some } f \in Q \\ &\iff (s', w) \vdash^*_{M'} (Q, \epsilon) \text{ with } Q \in F' \\ &\iff w \in L(M') \end{align*}\]

因此,w如果被NFA接受,那么它也被DFA接受,反之亦然.

下面我们来证明这个Claim,采用数学归纳法的方法

若$|w| = 0$,即$w = \epsilon$,那么
- 如果$(q, \epsilon) \vdash^*_M (p, \epsilon)$,那么$q = p$,我们想证明
  
  \[ (E(q), \epsilon) \vdash^*_{M'} (P, \epsilon) \]
  
  因为$M'$是决定性的,也就是说,对于给定的状态与给定的输入,只有一个可能的下一个状态.
  
  显然$(E(q), \epsilon) \vdash^*_{M'} (E(q), \epsilon)$,因此,取$P = E(q)$即可.
假设对于任意字符串$w$且$|w| = k$,Claim成立,即

\[ (q, w) \vdash^*_M (p, \epsilon) \iff \exists P \ni p,\ (E(q), w) \vdash^*_{M'} (P, \epsilon) \]
令$|w| = k+1$,$w = xa$,其中$a \in \Sigma$且$x \in \Sigma^*$且$|x| = k$.
- "=>":假设$(q, w) \vdash^*_M (p, \epsilon)$
  - 那么必然存在两个中间状态$r_1, r_2 \in Q$,使得
    
    \[ (q, xa) \vdash^*_M (r_1, a) \vdash^*_M (r_2, \epsilon) \vdash^*_M (p, \epsilon) \]
  - 由$(q, xa) \vdash^*_M (r_1, a)$可以得到$(q, x) \vdash^*_M (r_1, \epsilon)$,那么根据之前的归纳假设,我们有
    
    \[ \exists R_1 \ni r_1,\ (E(q), x) \vdash^*_{M'} (R_1, \epsilon) \]
  - 由$(r_1, a) \vdash^*_M (r_2, \epsilon)$可以得到$(r_1,a,r_2) \in \Delta$,那么根据上面等价DFA的定义,我们可以说$E(r_2) \subseteq \delta(R_1, a)$,因此,我们有
    
    \[ (E(q), xa) \vdash^*_{M'} (\delta(R_1, a), \epsilon) \]
  - 最后,$(r_2, \epsilon) \vdash^*_M (p, \epsilon)$,那么$p \in E(r_2)$
  \[\begin{align*} &\text{因此，} (E(q), xa) \vdash^*_{M'} (P, \epsilon) \\ &\text{其中 } P = \delta(R_1, a) \text{ 且 } p \in E(r_2) \subseteq P. \end{align*}\]
- "<=":假设$\exists P \ni p,\ (E(q), xa) \vdash^*_{M'} (P, \epsilon)$
  - 一样的,我们可以找到一个中间状态$R_1 \in Q'$,使得
    
    \[ (E(q), xa) \vdash^*_{M'} (R_1, a) \vdash^*_{M'} (P, \epsilon) \]
  - 显然我们有$P = \delta(R_1, a)$,取$p \in P$,那么根据上面的等价DFA的定义,我们有
    
    \[ \exists r_2 \in Q,\ p \in E(r_2) \text{ 且 } (r_1, a, r_2) \in \Delta \text{ for some } r_1 \in R_1 \]
  - 所以,就可以一连串地推出
    
    \[ (E(q), x) \vdash^*_{M'} (R_1, \epsilon) \Rightarrow (q, x) \vdash^*_M (r_1, \epsilon) , (r_1, a) \vdash^*_M (r_2, \epsilon) , (r_2, \epsilon) \vdash^*_M (p, \epsilon) \]
  - 因此,得到
    
    \[ (q, xa) \vdash^*_M (p, \epsilon) \]

FA & Regular Expression¶

一个语言是正则的,当且仅当它被某个有限自动机识别.

我们分成两个方向来进行证明

正则表达式 => FA¶

给定一个正则表达式,我们可以构造一个NFA来识别它.

我们知道,一个正则语言实际上是由空集$\emptyset$和单个字符$a \in \Sigma$通过正则运算(连接、并、闭包)构造出来的.

因此,证明的思路就是说明,对于能被一个FA接受的正则语言,在经过正则运算(连接、并、闭包)后,它仍然能被一个FA接受.由于空集和单个字符$a \in \Sigma$显然能被FA接受,因此我们只要证明Union,Concatenation, Kleene Star, complementation, intersection这五种运算在FA下封闭即可.

Union¶

假设有两个NFA,分别为$M_1 = (Q_1, \Sigma, \Delta_1, s_1, F_1)$和$M_2 = (Q_2, \Sigma, \Delta_2, s_2, F_2)$,它们分别识别语言$L(M_1)$和$L(M_2)$.

那么,我们可以构造一个新的NFA,使得它识别语言$L(M_1) \cup L(M_2)$.

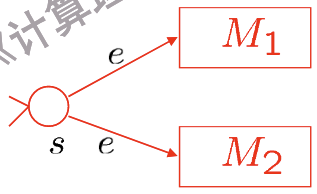
这个新的NFA为$M = (Q, \Sigma, \Delta, s, F)$,其中:

$Q = Q_1 \cup Q_2 \cup \{s\}$,其中$s$是一个新的初始状态.
$\Delta = \Delta_1 \cup \Delta_2 \cup \{(s, \epsilon, s_1), (s, \epsilon, s_2)\}$.
$F = F_1 \cup F_2$.

Union

Concatenation¶

假设有两个NFA,分别为$M_1 = (Q_1, \Sigma, \Delta_1, s_1, F_1)$和$M_2 = (Q_2, \Sigma, \Delta_2, s_2, F_2)$,它们分别识别语言$L(M_1)$和$L(M_2)$.

那么,我们可以构造一个新的NFA,使得它识别语言$L(M_1) \cdot L(M_2)$.

这个新的NFA为$M = (Q, \Sigma, \Delta, s, F)$,其中:

$Q = Q_1 \cup Q_2$.
$\Delta = \Delta_1 \cup \Delta_2 \cup \{(f, \epsilon, s_2) \mid f \in F_1\}$.
$s = s_1$.
$F = F_2$.

Concatenation

Kleene Star¶

假设有一个NFA,为$M_1 = (Q_1, \Sigma, \Delta_1, s_1, F_1)$,它识别语言$L(M_1)$.

那么,我们可以构造一个新的NFA,使得它识别语言$L(M_1)^*$.

这个新的NFA为$M = (Q, \Sigma, \Delta, s, F)$,其中:

$Q = Q_1 \cup \{s\}$,其中$s$是一个新的初始状态.
$\Delta = \Delta_1 \cup \{(s, \epsilon, s_1)\} \cup \{(f, \epsilon, s_1) \mid f \in F_1\}$.
$s = s$.
$F = F_1 \cup \{s\}$.

为什么需要一个新的初始状态?

在常规的想法下,我们把原来的初始状态也允许当终止状态,并让每个终止状态无条件地跳回初始状态,似乎就可以了.

但是,有反例:

令$L(M)=a(ab)^*$,那么$L(M)^*= (a(ab)^*)^*$.如果不引入新的初始状态,那么原来的初始状态是终止状态,因此,字符串$ab$就会被接受,但是$ab \notin (a(ab)^*)^*$.

Complementation¶

假设有一个DFA,为$M_1 = (Q_1, \Sigma, \delta_1, s_1, F_1)$,它识别语言$L(M_1)$.

我们可以构造一个新的DFA,为$M_2 = (Q_1, \Sigma, \delta_1, s_1, F_2)$,只要$F_2 = Q_1 - F_1$,这样,它识别语言$L(M_1)^c$.

Intersection¶

交集的思想类似于让两台自动机并行接受输入,只有当两个机器最后都到达终止状态时,输入才被接受.

我们使用笛卡尔积.

假设有两个DFA,分别为$M_1 = (Q_1, \Sigma, \delta_1, s_1, F_1)$和$M_2 = (Q_2, \Sigma, \delta_2, s_2, F_2)$,它们分别识别语言$L(M_1)$和$L(M_2)$.

那么,我们可以构造一个新的DFA,使得它识别语言$L(M_1) \cap L(M_2)$.

这个新的DFA为$M = (Q, \Sigma, \delta, s, F)$,其中:

$Q = Q_1 \times Q_2$.
$\delta((q_1, q_2), a) = (\delta_1(q_1, a), \delta_2(q_2, a))$.
$s = (s_1, s_2)$.
$F = F_1 \times F_2$.

FA => 正则表达式¶

首先,我们需要定义广义NFA(Generalized NFA, GNFA):

一个广义有限自动机 (Generalized Finite Automaton) $MG = (K_G, \Sigma_G, \Delta_G, s_G, F_G)$ 是对一个 NFA $M = (K, \Sigma, \Delta, s, F)$ 的如下泛化：

$MG$ 拥有单一的接受状态。
其字母表 $\Sigma_G = \Sigma \cup R_0$，其中 $R_0$ 是基于 $\Sigma$ 的正则表达式集合 $R$ 的一个有限子集。
$MG$ 的转移可以由符号或正则表达式来标记。
- 转移函数 $\Delta_G \subseteq K_G \times (\Sigma_G \cup \{\epsilon\} \cup R) \times K_G$
初始状态没有任何入边（指向它的转移），接受状态没有任何出边（从它出发的转移）。

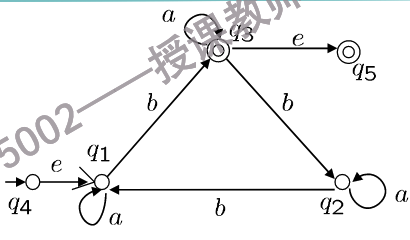
那么,把一个FA转换成一个等价的正则表达式,可以分为以下几个步骤:

重命名FA M的状态为$q_1, q_2, \ldots, q_{n-2}$
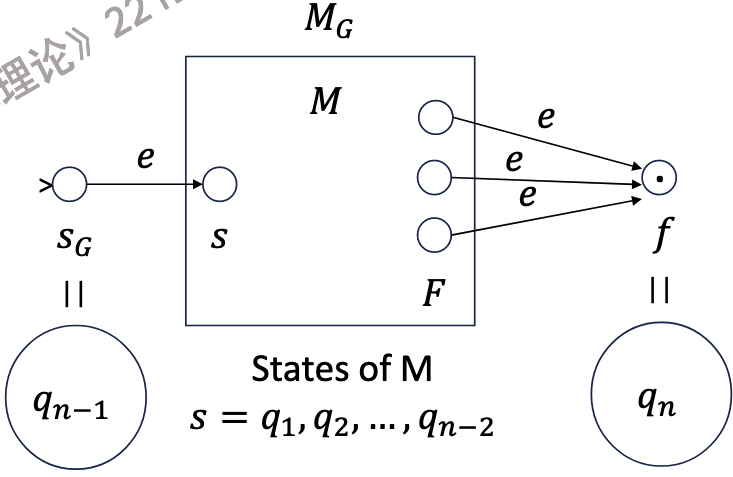
拓展M到MG:
- 增加两个状态$q_{n-1}, q_n$,其中$q_{n-1}$是新的初始状态,$q_n$是新的终止状态.
- $\Delta_G = \Delta \cup \{(q_{n-1}, \epsilon, q_1)\} \cup \{(f, \epsilon, q_n) \mid f \in F\}$
拓展FA到GNFA
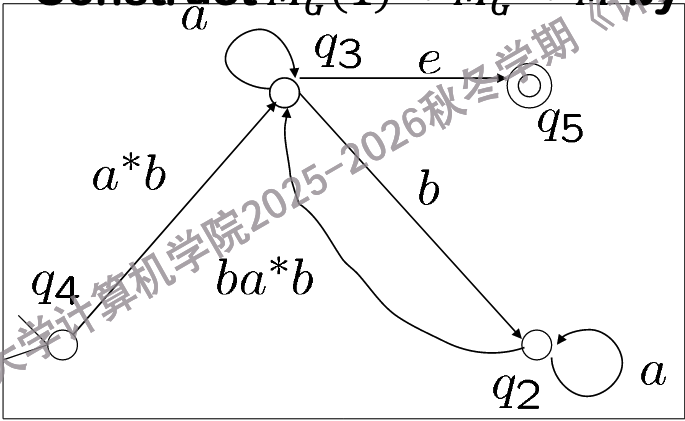
然后,不断消解中间状态,直到只剩下初始状态和终止状态.
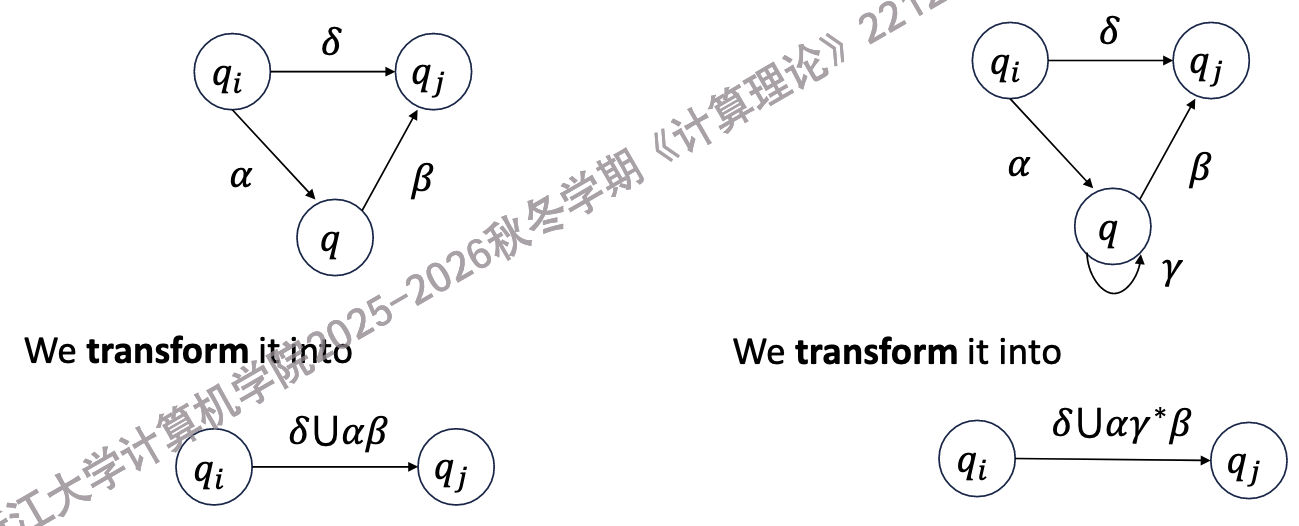
- 假设我们要消解$q_k$,那么,对于每一对状态$(q_i, q_j)$,我们需要找到所有从$q_i$到$q_j$的路径,这些路径可以分为三类:
  1. 直接从$q_i$到$q_j$的路径
  2. 从$q_i$到$q_k$,然后从$q_k$到$q_j$的路径
  3. 从$q_i$到$q_k$,然后在$q_k$上循环若干次,最后从$q_k$到$q_j$的路径
- 假设这些路径分别由正则表达式$r_1, r_2, r_3$表示,那么,我们可以把这些路径合并成一个新的正则表达式$r = r_1 \cup r_2 \cup r_3$,然后把$\Delta_G$中所有与$q_k$相关的转移删除,并增加一个新的转移$(q_i, r, q_j)$.
- 重复这个过程,直到只剩下初始状态和终止状态.
消解中间状态
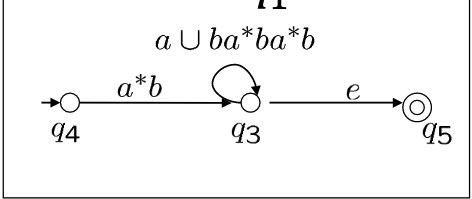
最后,我们得到一个只有两个状态的GNFA,其中唯一的转移标记着一个正则表达式,这个正则表达式就是我们要找的等价正则表达式.

Example

令M为FA,识别语言$L = \{\, w \in \{a, b\}^* \mid w \text{ 中的 } b \text{ 的个数为 } 3k+1,\, k \in \mathbb{N} \,\}$

初始FA拓展FA到GNFA消解中间状态q1消解中间状态q2消解中间状态q3,得到答案

初始FA

拓展FA到GNFA

消解中间状态q1

消解中间状态q2

消解中间状态q3

泵定理¶

既然我们已经知道正则语言和有限自动机是等价的,那么我们可以用直觉的语言表述,一个语言如果需要“无限的记忆”，那么它就不是正则语言,因为为了表示这无限的记忆,需要无限的状态,而有限自动机只有有限的状态.

什么是无限的记忆? 比如,语言$L = \{a^n b^n \mid n \geq 0\}$,它要求字符串中'a'和'b'的数量相等.那么,当一个字符串输入的时候,我们需要记住现在有几个'a',每一个数量对应一个状态,以便后面能匹配相等数量的'b'.但是,由于有限自动机的状态是有限的,所以它无法记住任意数量的'a'.因此,这个语言不是正则语言.

但是,如果要识别有偶数个'a'的字符串,那么我们只需要两个状态:一个表示当前有偶数个'a',另一个表示当前有奇数个'a'.每次输入'a'时,状态在这两个状态之间切换.因此,这个语言是正则语言.

泵定理已经在之前讲述过.

Example

例1例2

证明:$L = \{a^n |n是质数\}$不是正则语言.

假设$L$是正则语言,那么根据泵定理,存在一个泵长度$p$,使得对于任意字符串$s \in L$且$|s| \geq p$,都可以把$s$分解为$s = xyz$,其中$x=a^k, y=a^m, z=a^p$,$k+m+p\text{是质数}$

那么,$xy^iz = a^{k+im+p}$也必须在$L$中,即$k+im+p$是质数.

然而,这是不成立的,取$i = k + p$,那么

\[ k + (k + p)m + p = (k + p)(m + 1) \]

显然,$(k + p)(m + 1)$不是质数,与假设矛盾.

$L = \{w \in \{a, b\}^* | w \text{ 中 } a \text{ 和 } b \text{ 的数量相等}\}$不是正则语言.

若$L$是正则语言,那么根据交集的封闭性,我们有$L \cap a^* b^* = \{a^n b^n | n \geq 0\}$也是正则语言.

但是,我们已经知道$\{a^n b^n | n \geq 0\}$不是正则语言,因此,与假设矛盾.

自动机(Automata)¶

DFA(Deterministic Finite Automata)¶

NFA(Nondeterministic Finite Automata)¶

定义¶

Claim¶

FA & Regular Expression¶

正则表达式 => FA¶

Union¶

Concatenation¶

Kleene Star¶

Complementation¶

Intersection¶

FA => 正则表达式¶

泵定理¶

评论