跳转至

CFL与PDA

约 5384 个字 2 张图片 预计阅读时间 27 分钟

我们已经知道,形如 a^n b^n 的语言不是正则语言,但这种语言很容易使用一种递归的方式来定义.

显然\(\epsilon\)属于该语言,并且如果 w 属于该语言,那么 a w b 也属于该语言.

为了描述这种语言,我们引入了上下文无关文法(CFG).

Context-Free Grammars

一个上下文无关文法是一个四元组\(G=(V, T, P, S)\),其中

  • V 是一个有限的非终结符号集合.

  • T 是一个有限的终结符号集合,且\(V \cap T = \emptyset\).

  • P 是一个有限的产生式集合,每个产生式的形式为\(A \rightarrow \alpha\),其中\(A \in V\)且\(\alpha \in (V \cup T)^*\).

  • S 是一个特殊的非终结符号,称为开始符号,且\(S \in V\).

之所以称为上下文无关文法,是因为我们总是可以无条件的将非终结符号替换为其产生式右边的符号串,而不考虑该非终结符号在字符串中的上下文环境.

比如,在最开始的例子中,我们可以将\(S\)替换为\(a S b\)或者\(\epsilon\),而不考虑\(S\)前后的符号是什么,就像宏替换一样.

所有正则语言都是上下文无关语言

考虑一个DFA\(M=(Q, \Sigma, \delta, q_0, F)\),我们可以构造一个CFG\(G=(V, T, P, S)\),使得\(L(G)=L(M)\).

具体地,我们定义:

  • \(V = Q\).

  • \(T = \Sigma\).

  • 对于每个状态\(q \in Q\)和输入符号\(a \in \Sigma\),如果\(\delta(q, a) = p\),则在\(P\)中添加产生式\(q \rightarrow a p\).

  • 对于每个接受状态\(f \in F\),在\(P\)中添加产生式\(f \rightarrow \epsilon\).

Remark

  1. 对于任意字符串 \(u, v \in V^{*}\)，有：

    • \(u \Rightarrow_{G} v \iff \exists\, x, y \in {(V+T)}^{*},\ A \in V,\ \text{使得 } u = x A y,\ v = x v' y,\ \text{且 } A \rightarrow_{G} v'\)

    • \(\Rightarrow_{G}^{*}\) 是 \(\Rightarrow_{G}\) 的自反且传递闭包

  2. G 中从 \(w_{0}\) 推导出 \(w_{n}\) 的一个推导过程为：

    \[ w_{0} \Rightarrow_{G} w_{1} \Rightarrow_{G} \cdots \Rightarrow_{G} w_{n} \]

    其中 \(n\) 称为该推导的长度

  3. G 所生成的语言定义为：

    \[ L(G) = \{\, w \in \Sigma^{*} \mid S \Rightarrow_{G}^{*} w \,\} \]
    • 因此,上下文无关语言是指可以被某个上下文无关文法生成的语言集合.

证明\(L=L(G)\)

还是以最开头的式子\(L=\{a^n b^n | n \geq 0\}\)为例,我们可以构造一个CFG\(G=(V, T, P, S)\),满足:

  • \(S = S,T = {a, b}, V = {S}\)

  • \(P\)包含以下产生式:

    • \(S \rightarrow a S b\)

    • \(S \rightarrow \epsilon\)

    • \(S \rightarrow SS\)

    • \(S \rightarrow b S a\)

为什么需要\(S \rightarrow SS\)

没有这个表达式,我们就无法生成形如\(abba\)的字符串

  1. \(w \in L \Rightarrow w \in L(G)\)

    证明:使用数学归纳法.

    • 当\(n=0\)时,\(w=\epsilon\),显然\(S \Rightarrow \epsilon\),所以\(\epsilon \in L(G)\).

    • 假设当\(n=k\)时,对于任意\(w \in L\)都有\(w \in L(G)\)成立.现在考虑\(n=k+2\)的情况.对于\(n=k+2\)的字符串\(x\),有四种表现形式:

      • \(x = a y b\),其中\(y\)的长度为\(k\).根据归纳假设,\(y \in L(G)\),所以\(S \Rightarrow a S b \Rightarrow^* a y b = x\),因此\(x \in L(G)\).

      • \(x = b y a\),和第一种类似

      • \(x = a y a\),我们总是可以将\(y\)分成\(u v\)两部分,使得这两部分中b的个数都比a多一个,则\(au,va \in L\),根据归纳假设,\(S \Rightarrow^* au\)且\(S \Rightarrow^* va\),所以\(S \Rightarrow SS \Rightarrow^* au va = x\),因此\(x \in L(G)\).

      • \(x = b y b\),和第三种类似.

  2. \(w \in L(G) \Rightarrow w \in L\) 我们以推导长度来进行数学归纳法.

    • 当推导长度为1时,显然只能是\(S \Rightarrow \epsilon\),所以\(\epsilon \in L\).

    • 假设对于所有推导长度小于等于\(n\)的字符串\(w \in L(G)\)都有\(w \in L\)成立.现在考虑推导长度为\(n+1\)的字符串\(x\).根据产生式的定义,有以下几种情况:

      • \(S \Rightarrow a S b \Rightarrow^* x\),则\(x\)的形式为\(a y b\),其中\(y\)的推导长度为\(n\).根据归纳假设,\(y \in L\),所以\(x \in L\).

      • \(S \Rightarrow b S a \Rightarrow^* x\),和第一种类似.

      • \(S \Rightarrow SS \Rightarrow^* x\),则\(x\)可以分成\(u v\)两部分,使得\(S \Rightarrow^* u\)且\(S \Rightarrow^* v\).根据归纳假设,\(u, v \in L\),所以\(x \in L\).

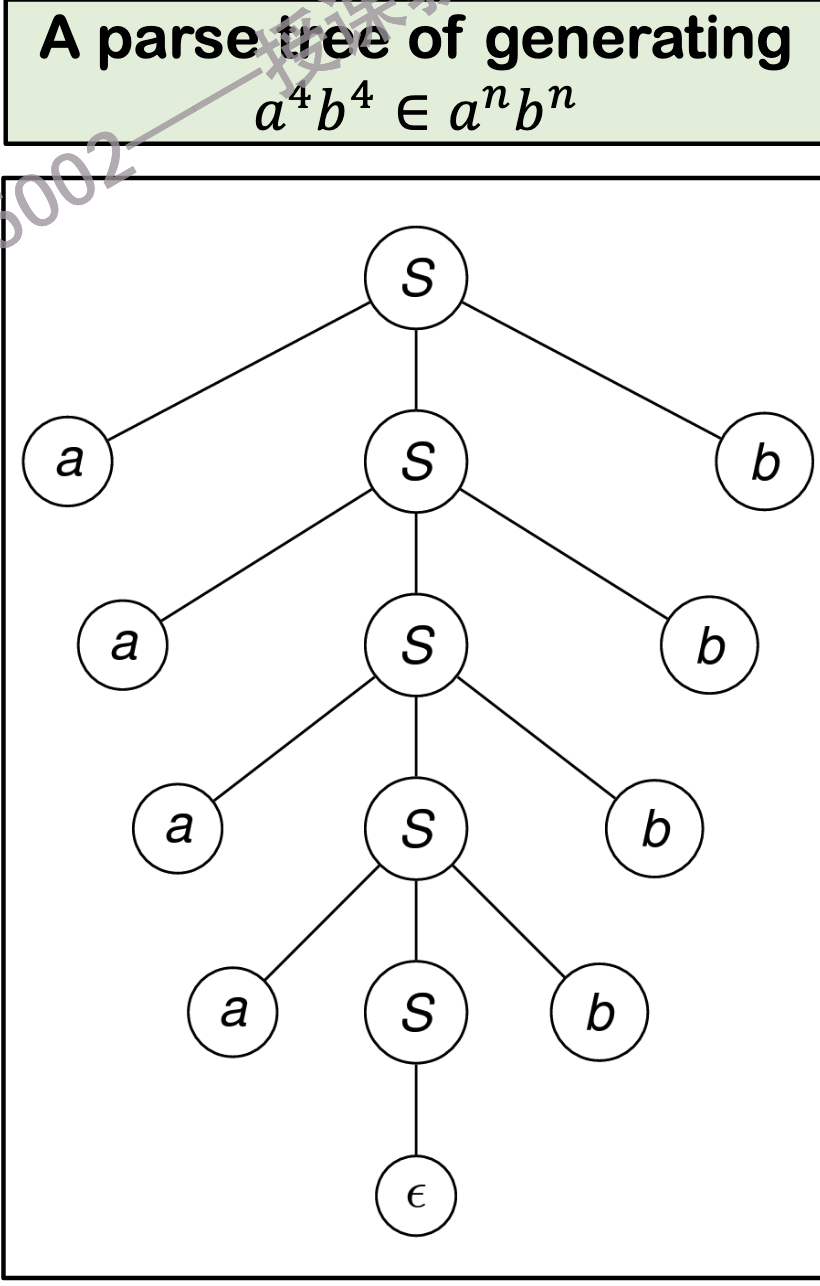
Parse Trees

一个字符串的解析树(或语法树)是一个树形结构,用于表示该字符串是如何根据某个上下文无关文法生成的.

  • 树的根节点表示开始符号.

  • 内部节点表示非终结符号.

  • 叶子节点表示终结符号.

Remark

  1. 从叶子节点按从左到右顺序读出来的符号串就是该解析树所表示的字符串.

  2. 终结符只能出现在叶子节点，不能出现在中间过程节点.

  3. 非终结符只能出现在中间过程节点，不能出现在叶子节点.

Parse Tree
解析树示例

Similarity

对于两个推导序列 \(D = (x_0, x_1, \ldots, x_n)\) 和 \(D' = (x'_0, x'_1, \ldots, x'_n)\)，我们说 \(D\) precedes \(D'\)，记作 \(D \prec D'\)，当且仅当存在 \(1 \leq k \leq n\)，使得：

  • 对所有 \(i \neq k\)，都有 \(x_i = x'_i\)

  • \(x_{k-1} = x'_{k-1} = uAvBw\)，其中 \(u, v, w \in {(V+\Sigma)}^*\)，\(A, B \in V\)

  • \(x_k = uyvBw\)，其中 \(A \rightarrow y \in R\)

  • \(x'_k = uAvzw\)，其中 \(B \rightarrow z \in R\)

  • \(x_{k+1} = x'_{k+1} = uyvzw\)

那么,我们称\(D\)和\(D'\)是相似的,当它们是precedes的自反,对称且传递闭包时.

相似的推导序列对应同一棵解析树.

  • Leftmost Derivation: 在每一步推导中,总是选择最左边的非终结符进行替换.

  • Rightmost Derivation: 在每一步推导中,总是选择最右边的非终结符进行替换.

设 \(G = (V, \Sigma, R, S)\) 是一个上下文无关文法（CFG），\(A \in V - \Sigma\)，\(w \in \Sigma^*\)。则我们总是认为以下论述是等价的:

  • \(A \Rightarrow^* w\)

  • 存在一个以 \(A\) 为根、以 \(w\) 为叶子读出的解析树（Parse tree）

  • 存在一个从 \(A\) 到 \(w\) 的最左推导（leftmost derivation），记作 \(A \Rightarrow_{lm}^* w\)

  • 存在一个从 \(A\) 到 \(w\) 的最右推导（rightmost derivation），记作 \(A \Rightarrow_{rm}^* w\)

Ambiguous Grammar

如果一个上下文无关文法\(G\)存在某个字符串\(w \in L(G)\),使得\(w\)有两棵不同的解析树,则称该文法是二义性的(ambiguous).

否则,称该文法是无二义性的(unambiguous).

二义性的文法允许多个最左推导和多个最右推导.

Pushdown Automata

感性地说,下推自动机吃掉输入来变换栈的内容,并根据栈的内容来决定是否接受输入.

下推自动机实际上是一种带有栈存储结构的有限状态自动机.

定义如下:

一个下推自动机(PDA)是一个六元组\(M=(Q, \Sigma, \Gamma, \delta, q_0, F)\),其中:

  • Q 是一个有限状态集合.

  • \(\Sigma\) 是一个有限输入符号集合,称为输入字母表.

  • \(\Gamma\) 是一个有限栈符号集合,称为栈字母表.

  • \(\delta\) 是一个状态转移函数,其形式为\(\delta: Q \times (\Sigma \cup \{\epsilon\}) \times \Gamma^* \rightarrow Q \times \Gamma^*\)

  • \(q_0 \in Q\) 是初始状态.

  • \(F \subseteq Q\) 是接受状态集合.

下推自动机接受一个字符串\(w \in \Sigma^*\),如果存在一种状态转换序列,使得:

  1. 初始状态为\(q_0\).

  2. 输入字符串被完全读取.

  3. 栈在读取结束时为空.

  4. 最终状态为接受状态.

Example

我们要设计一个PDA来识别语言\(L=\{w c w^R,w=\{a,b\}^*\}\).

我们令:

  • \(Q = \{s,f\}\)

  • \(\Sigma = \{a,b,c\}\)

  • \(\Gamma = \{a,b\}\)

  • 初始状态\(q_0 = s\)

  • 接受状态\(F = \{f\}\)

  • 状态转移函数\(\delta\)定义如下:

    • \((s,a,e) \rightarrow (s,a)\)

    • \((s,b,e) \rightarrow (s,b)\)

    • \((s,c,e) \rightarrow (f,e)\)

    • \((f,a,a) \rightarrow (f,e)\)

    • \((f,b,b) \rightarrow (f,e)\)

PDA Example
PDA示例

注意,形如\((q_i, a, X) \rightarrow (q_j, Y)\)代表了在状态\(q_i\)下,当读取输入符号\(a\)且栈顶符号为\(X\)时,转移到状态\(q_j\),并将栈顶符号\(X\)替换为符号串\(Y\).

Configuration of PDA

下推自动机的配置(configuration)是一个三元组\((q, w, \gamma)\),其中:

  • \(q \in Q\) 是当前状态.

  • \(w \in \Sigma^*\) 是剩余输入字符串.

  • \(\gamma \in \Gamma^*\) 是当前栈内容,栈顶符号在字符串的最左侧.

PDA从配置\((q_i, a w, X \beta)\)转移到配置\((q_j, w, Y \beta)\),如果存在转移规则\((q_i, a, X) \rightarrow (q_j, Y)\),记作\((q_i, a w, X \beta) \vdash_M (q_j, w, Y \beta)\).

CFL与PDA等价性

和正则语言与有限状态自动机的等价性类似,上下文无关语言与下推自动机也是等价的.

Claim

设 \(w \in \Sigma^*\) 且 \(\alpha\) 是一个非终结符串（或空串 \(\epsilon\)），即 \(\alpha \in (V \setminus \Sigma)^* \cup \{\epsilon\}\)。

对于一个从文法 \(G\) 构造出的下推自动机 \(M\)，以下关系成立：

文法 \(G\) 中的最左推导 \(S \Rightarrow_{lm}^* w\alpha\) 成立，当且仅当自动机 \(M\) 中存在计算过程 \((q, w, S) \vdash_M^* (q, \epsilon, \alpha)\)。

\[ S \Rightarrow_{lm}^* w\alpha \iff (q, w, S) \vdash_M^* (q, \epsilon, \alpha) \]

这个论断足以证明 \(L(G) = L(M)\)。当取 \(\alpha = \epsilon\) 时，我们得到：

\[ S \Rightarrow_{lm}^* w \iff (q, w, S) \vdash_M^* (q, \epsilon, \epsilon) \]

这表明，一个字符串 \(w\) 能由文法 \(G\) 生成，当且仅当它能被自动机 \(M\) 接受。因此，\(w \in L(G) \iff w \in L(M)\)。

实际上,CFL和PDA之间是一个相互转换的过程.CFL产生一个字符串,而PDA则是识别一个字符串.

PDA的接受一个字符串的数学表达为:\((q, w, S) \vdash_M^* (q, \epsilon, \epsilon)\).相当于S是待匹配内容,而w是输入内容.每匹配一部分,就删去待匹配内容与输入内容的对应部分,直到两者都为空.

普遍的规律是,对于一个上下文无关文法 \(G = (V, \Sigma, R, S)\)，我们可以构造一个下推自动机 \(M = (K, \Sigma, \Gamma, \Delta, s, F)\)，使得 \(L(M) = L(G)\)：

  • PDA \(M\) 只有两个状态：\(p\)（初始状态）和 \(q\)（最终状态）。

  • 栈字母表 \(\Gamma = V\)。

  • \(\Delta\) 包含以下转移规则：

    • \((p, \epsilon, \epsilon) \rightarrow (q, S)\)

    • 对于每个产生式 \(A \rightarrow x \in R\)，有 \((q, \epsilon, A) \rightarrow (q, x)\)

    • 对于每个终结符 \(a \in \Sigma\)，有 \((q, a, a) \rightarrow (q, \epsilon)\)

从 CFG 到 PDA 的转换示例

设上下文无关文法 \(G = (V, \Sigma, R, S)\)，其中：

  • \(V = \{S, a, b, c\}\)

  • \(\Sigma = \{a, b, c\}\)

  • \(R = \{S \rightarrow aSa, S \rightarrow bSb, S \rightarrow c\}\)

那么该文法生成的语言 \(L(G) = \{wcw^R \mid w \in \{a, b\}^*\}\)。

根据上述构造方法，对应的下推自动机 \(M = (K, \Sigma, V, \Delta, s, F)\) 为：

  • \(K = \{p, q\}\)

  • \(s = p\)

  • \(F = \{q\}\)

  • \(\Delta\) 包含以下转移规则：

    • \((p, \epsilon, \epsilon) \rightarrow (q, S)\)

    • \((q, a, a) \rightarrow (q, \epsilon)\)

    • \((q, b, b) \rightarrow (q, \epsilon)\)

    • \((q, c, c) \rightarrow (q, \epsilon)\)

    • \((q, \epsilon, S) \rightarrow (q, aSa)\)

    • \((q, \epsilon, S) \rightarrow (q, bSb)\)

    • \((q, \epsilon, S) \rightarrow (q, c)\)

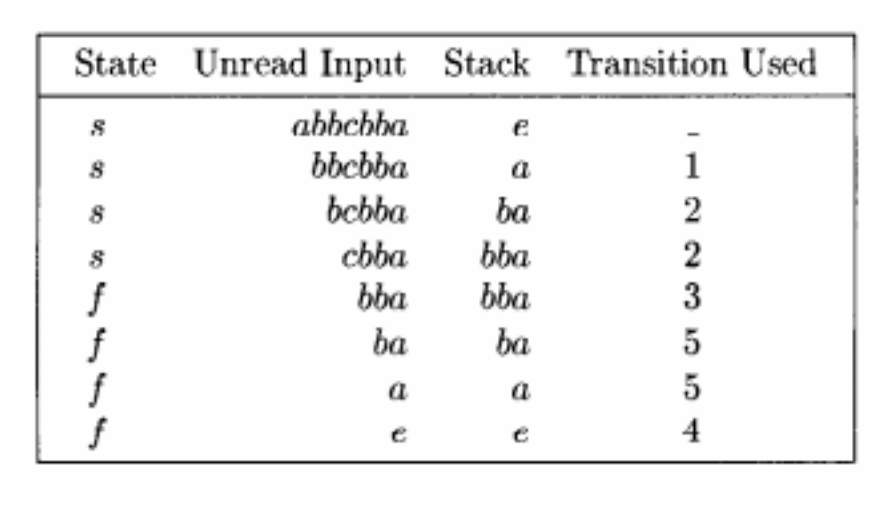
现在，我们来考虑字符串 abbcbba：

  • 最左推导过程: \(S \Rightarrow aSa \Rightarrow abSba \Rightarrow abbSbba \Rightarrow abbcbba\)

  • PDA 对应的计算过程:

    \[\begin{aligned} (p,\, abbcbba,\, \epsilon) &\vdash (q,\, abbcbba,\, S) \\ &\vdash (q,\, abbcbba,\, aSa) \\ &\vdash (q,\, bbcbba,\, Sa) \\ &\vdash (q,\, bbcbba,\, bSba) \\ &\vdash (q,\, bcbba,\, Sba) \\ &\vdash (q,\, bcbba,\, bSbba) \\ &\vdash (q,\, cbba,\, Sbba) \\ &\vdash (q,\, cbba,\, cbba) \\ &\vdash^{*} (q,\, \epsilon,\, \epsilon) \end{aligned}\]

最终，输入字符串被完全读取，栈为空，且 PDA 处于接受状态 \(q\)，因此字符串 abbcbba 被接受。

下面我们需要证明这个Claim

\(\rightarrow\) 方向

证明：\(S \Rightarrow_{lm}^* w\alpha \implies (q, w, S) \vdash_M^* (q, \epsilon, \alpha)\)

我们对最左推导的长度进行数学归纳。

基础步骤 (Basis Step):

  • 当推导长度为 0 时，推导为 \(S \Rightarrow^0 S\)。
  • 此时，\(w = \epsilon\) 且 \(\alpha = S\)。
  • 对应的 PDA 计算为 \((q, \epsilon, S) \vdash_M^0 (q, \epsilon, S)\)，这是自反的，因此成立。

归纳假设 (Induction Hypothesis):

  • 假设对于所有长度小于或等于 \(n\)（\(n \geq 0\)）的最左推导 \(S \Rightarrow_{lm}^* w\alpha\)，都有 \((q, w, S) \vdash_M^* (q, \epsilon, \alpha)\) 成立。

归纳步骤 (Induction Step):

  • 考虑一个长度为 \(n+1\) 的最左推导： $$ S = u_0 \Rightarrow_{lm} u_1 \Rightarrow_{lm} \dots \Rightarrow_{lm} u_n \Rightarrow_{lm} u_{n+1} = w\alpha $$
  • 设 \(u_n = xA\beta\)，其中 \(A\) 是 \(u_n\) 中最左边的非终结符，\(x \in \Sigma^*\)。
  • 那么，推导的最后一步必然是应用了某个产生式 \(A \rightarrow \gamma\)，使得 \(u_{n+1} = x\gamma\beta\)。
  • 此时，我们有了一个长度为 \(n\) 的最左推导：\(S \Rightarrow_{lm}^* u_n = xA\beta\)。
  • 根据归纳假设，我们可以得出： $$ (q, x, S) \vdash_M^* (q, \epsilon, A\beta) \quad \cdots \quad (1) $$
  • 根据 PDA 的构造规则，由于存在产生式 \(A \rightarrow \gamma\)，PDA 中必然有转移规则 \((q, \epsilon, A) \rightarrow (q, \gamma)\)。这使得 PDA 可以进行如下计算： $$ (q, \epsilon, A\beta) \vdash_M (q, \epsilon, \gamma\beta) \quad \cdots \quad (2) $$
  • 结合 (1) 和 (2)，我们得到： $$ (q, x, S) \vdash_M^* (q, \epsilon, \gamma\beta) $$
  • 由于 \(u_{n+1} = x\gamma\beta = w\alpha\)，且 \(x\) 是 \(w\) 的前缀，我们可以设 \(w = xy\)，其中 \(y \in \Sigma^*\)。
  • 那么，\(\gamma\beta\) 必然等于 \(y\alpha\)。
  • 我们可以将上面的 PDA 计算过程重写为： $$ (q, w, S) = (q, xy, S) \vdash_M^* (q, y, \gamma\beta) = (q, y, y\alpha) \quad \cdots \quad (3) $$
  • PDA 在读取完 \(y\) 之后，会到达配置 \((q, \epsilon, \alpha)\)： $$ (q, y, y\alpha) \vdash_M^* (q, \epsilon, \alpha) \quad \cdots \quad (4) $$
  • 结合 (3) 和 (4)，我们最终得到 \((q, w, S) \vdash_M^* (q, \epsilon, \alpha)\)。
  • 归纳步骤完成。

\(\leftarrow\) 方向

证明的思路是,从一个下推自动机出发,构造出一个对应的上下文无关文法.

证明：\((q, w, S) \vdash_M^* (q, \epsilon, \alpha) \implies S \Rightarrow_{lm}^* w\alpha\)

我们称一个下推自动机(PDA)是简单的 (simple), 如果它满足以下条件：

对于任意一个转移规则 \((q, a, \beta) \rightarrow (p, \gamma)\)，如果 \(q\) 不是初始状态，那么该转移必须满足：

  • \(\beta \in \Gamma\) （即 \(\beta\) 是单个栈符号）

  • \(|\gamma| \leq 2\) （即 \(\gamma\) 的长度最多为2）

换句话说，一个简单的PDA总是：

  • 只查看其栈顶的单个符号。

  • 将栈顶符号替换为空串 \(\epsilon\)、单个栈符号或两个栈符号。

为了便于后续证明，我们把任意 PDA 规约为一个等价的“简单 PDA” \(M'\)。除一条特殊的启动规则外，\(M'\) 的每条转移都满足“弹出 1 个栈符号，压入 0/1/2 个栈符号”。

  1. 规范化启动与接受

    为 PDA 增加唯一的新初始状态 \(s'\)、唯一的新接受状态 \(f'\)，以及新的栈底标记 \(Z\)。

    • 启动规则：添加 \((s', \varepsilon, \varepsilon) \to (s, Z)\)。
      这是 \(M'\) 的唯一启动动作：先把 \(Z\) 压入栈，再跳到原初始状态 \(s\)；此后栈永不真正“见底”。

    • 接受规则：对原 PDA 的每个接受状态 \(f \in F\)，添加 \((f, \varepsilon, Z) \to (f', \varepsilon)\)。
      这是 \(M'\) 的唯一接受方式：当输入读尽且栈仅剩 \(Z\) 时，弹出 \(Z\) 并转入新的接受状态 \(f'\)。

  2. 将一般转移规约为“简单”格式

    • 步骤 1：修复“弹出过多”（pop > 1）
      若存在一次弹出多个符号的规则 $$ (q, a, B_1\cdots B_n)\to(p,\gamma), $$ 则将其拆为逐个弹出的链式规则 $$ \begin{aligned} (q, \varepsilon, B_1) &\to (q_1, \varepsilon)\ (q_1, \varepsilon, B_2) &\to (q_2, \varepsilon)\ & \vdots \ (q_{n-1}, a, B_n) &\to (p, \gamma). \end{aligned} $$

    • 步骤 2：修复“压入过多”（push > 2）
      若存在一次压入 \(m>2\) 个符号的规则 $$ (q, a, B)\to(p, C_1C_2\cdots C_m), $$ 则分解为每步最多压入两个符号： $$ \begin{aligned} (q, a, B) &\to (r_1, C_1C_2)\ (r_1, \varepsilon, \varepsilon) &\to (r_2, C_3)\ & \vdots \ (r_{m-2}, \varepsilon, \varepsilon) &\to (p, C_m). \end{aligned} $$ 注意：这里临时引入了“弹出 0”的规则，下一步统一修复。

    • 步骤 3：修复“弹出为零”（pop = 0）
      若存在不弹出栈符号的规则 $$ (q, a, \varepsilon)\to(p,\gamma), $$ 则对每一个栈符号 \(A\)（包括栈底符号 \(Z\)）用等效的“先弹后压”形式替换： $$ (q, a, A)\to(p, \gamma A), \qquad \forall\, A\in \Gamma \cup {Z}. $$ 这样其净效应等价于在栈顶符号 \(A\) 上方压入 \(\gamma\)，同时形式上满足“弹出 1、压入 \(\le 2\)”的简单规则要求。

我们的目标是构造一个上下文无关文法（CFG）\(G\)，使其生成的语言与给定的简单 PDA \(M'\) 接受的语言相同。

  1. 定义非终结符

    文法的非终结符 \(V\) 由一个新的起始符号 \(S\) 和一系列形如 \(\langle q, A, p \rangle\) 的三元组构成，其中：

    • \(q, p\) 是 PDA 的状态。

    • \(A\) 是一个栈符号。

    含义：非终结符 \(\langle q, A, p \rangle\) 旨在生成所有能让 PDA 从状态 \(q\)（栈顶为 \(A\)）开始，经过一系列转移，最终到达状态 \(p\) 并恰好将 \(A\) 从栈中弹出的输入字符串 \(w\)。

    \[ \langle q, A, p \rangle \Rightarrow^* w \iff (q, w, A) \vdash_{M'}^* (p, \varepsilon, \varepsilon) \]

  2. 定义产生式规则

    我们根据简单 PDA \(M'\) 的转移规则来定义 CFG \(G\) 的产生式 \(R\)，分为以下四种类型：

    1. 起始规则

      • 对于 PDA 的新初始状态 \(s'\)、原初始状态 \(s\)、新栈底符号 \(Z\) 和新接受状态 \(f'\)，我们添加规则：
      \[ S \to \langle s, Z, f' \rangle \]
      • 这条规则的含义是：整个语言的生成过程，等价于 PDA 从原初始状态 \(s\)（栈底为 \(Z\)）开始，最终到达接受状态 \(f'\) 并清空栈的过程。

    2. 弹出规则 (Pop)

      • 对于 \(M'\) 中形如 \((q, a, B) \to (r, \varepsilon)\) 的转移（弹出 \(B\)，不压入任何符号），我们添加规则：
      \[ \langle q, B, r \rangle \to a \]

    3. 替换规则 (Replace)

      • 对于 \(M'\) 中形如 \((q, a, B) \to (r, C)\) 的转移（弹出 \(B\)，压入 \(C\)），我们为每一个可能的状态 \(p \in K'\) 添加规则：
      \[ \langle q, B, p \rangle \to a \langle r, C, p \rangle \]

    4. 压入规则 (Push)

      • 对于 \(M'\) 中形如 \((q, a, B) \to (r, C_1C_2)\) 的转移（弹出 \(B\)，压入 \(C_1C_2\)），我们为每一对可能的状态 \(p, p' \in K'\) 添加规则：
      \[ \langle q, B, p \rangle \to a \langle r, C_1, p' \rangle \langle p', C_2, p \rangle \]

Languages that are and are not CF

和正则语言一样,我们必须先知道CFL在并集,连接和闭包下是封闭的.

那么,也就是说,CFL在交集和补集下是不封闭的.

Remark

  • 回顾一下正则语言在交集运算下的封闭性：

    • 构造等价的DFA需要自动机是确定性的。

    • 补集运算同样要求自动机是确定性的。

    • \(L_1 \cap L_2 = \overline{\overline{L_1} \cup \overline{L_2}}\)

  • 并非所有的上下文无关语言都能被一个确定性下推自动机（DPDA）接受，因此 CFL 在交集和补集运算下不封闭。

示例

  • \(L_1 = \{a^n b^n c^m \mid m, n \ge 0\} = \{a^n b^n \mid n \ge 0\} \circ c^*\)

  • \(L_2 = \{a^m b^n c^n \mid m, n \ge 0\} = a^* \circ \{b^n c^n \mid n \ge 0\}\)

  • \(L_1\) 和 \(L_2\) 都是上下文无关语言，但它们的交集 \(L_1 \cap L_2 = \{a^n b^n c^n \mid n \ge 0\}\) 不是上下文无关语言。

但是,一个CFL和一个正则语言的交集仍然是一个CFL.

Pumping Lemma for CFL

令\(L\)为一个上下文无关语言,则存在一个整数\(p \geq 1\),使得对于任意字符串\(s \in L\)且\(|s| \geq p\),都可以将\(s\)分成五个子串\(s = uvwxy\),满足:

  1. 对于任意整数\(i \geq 0\),字符串\(uv^i w x^i y \in L\).

  2. \(|v x| \geq 1\).

  3. \(|vwx| \leq p\)。

使用Pumping Lemma证明某语言不是CFL

证明语言\(L = \{a^n b^n c^n \mid n \geq 0\}\)不是上下文无关语言.

假设\(L\)是一个上下文无关语言,则存在一个整数\(p \geq 1\),使得对于任意字符串\(s \in L\)且\(|s| \geq p\),都可以将\(s\)分成五个子串\(s = uvwxy\),满足Pumping Lemma的条件.

现在,我们选择字符串\(s = a^p b^p c^p \in L\),显然\(|s| = 3p \geq p\).

根据Pumping Lemma,我们可以将\(s\)分成五个子串\(s = uvwxy\),满足:

  1. 对于任意整数 \(i \geq 0\)，字符串 \(uv^i w x^i y \in L\)。

  2. \(|vx| \geq 1\)。

  3. \(|vwx| \leq p\)。

由于 \(|vwx| \leq p\)，子串 vwx 只能是 a...a、b...b、c...c、a...ab...b 或 b...bc...c 的形式。它不可能同时包含 a 和 c，因为 a 和 c 之间被 p 个 b 隔开。

现在我们分情况讨论 vx 中包含的符号种类：

  1. vx 只包含一种符号

    • vx 只能由 a、b 或 c 组成。
    • 考虑字符串 \(uv^2wx^2y\)。由于 \(|vx| \geq 1\)，这个新字符串中至少有一种符号的数量增加了，而其他两种符号的数量保持不变。
    • 因此，新字符串不再满足 a、b、c 数量相等的要求，即 \(uv^2wx^2y \notin L\)。这与条件1矛盾。

  2. vx 包含两种符号

    • 根据 \(|vwx| \leq p\) 的限制，vx 只能包含 a 和 b，或者 b 和 c。
    • 情况一：vx 包含 a 和 b。
      • 考虑字符串 \(uv^2wx^2y\)。这个新字符串中 a 和 b 的数量增加了，但 c 的数量不变。因此，它不属于 \(L\)。这与条件1矛盾。
      • 另外，如果 v 或 x 中任何一个同时包含 a 和 b (例如 v = ab)，那么 \(uv^2wx^2y\) 会出现 ...ab...ab... 这样的子串，破坏了 \(a^n b^n c^n\) 的顺序，同样不属于 \(L\)。
    • 情况二：vx 包含 b 和 c。
      • 同理，泵操作会破坏符号数量的平衡或顺序。

由于所有可能的情况都会导致矛盾，因此我们的初始假设“\(L\) 是一个上下文无关语言”是错误的。

评论