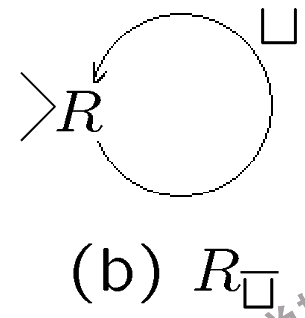图灵机¶

约 6495 个字 6 行代码 12 张图片预计阅读时间 33 分钟

FA只能读取纸带上的内容并转移状态,PDA可以读取纸带上的内容并操作栈顶,而图灵机则可以读取纸带上的内容并对纸带进行读写操作.这意味着图灵机是最强大的自动机,任何可以被计算的问题都可以被图灵机解决.

图灵机

图灵机是一个五元组\(M=(K,\Sigma,\delta,s,H)\),其中:

\(K\) 是一个有限的状态集。
\(\Sigma\) 是一个字母表，其中：
- 包含 \(\sqcup\) (空白符号) 和 \(\triangleright\) (左端符号)。
- 不包含符号 \(\rightarrow\) 和 \(\leftarrow\)。
\(s \in K\) 是初始状态。
\(H \subseteq K\) 是停机状态集。
\(\delta: (K - H) \times \Sigma \to K \times (\Sigma \cup \{\leftarrow, \rightarrow\})\) 是转移函数，满足：
- 对于任意 \(q \in K - H\)，如果 \(\delta(q, \triangleright) = (p, b)\)，那么 \(b = \rightarrow\)。
- 对于任意 \(q \in K - H\) 和 \(a \in \Sigma\)，如果 \(\delta(q, a) = (p, b)\)，那么 \(b \neq \triangleright\)。

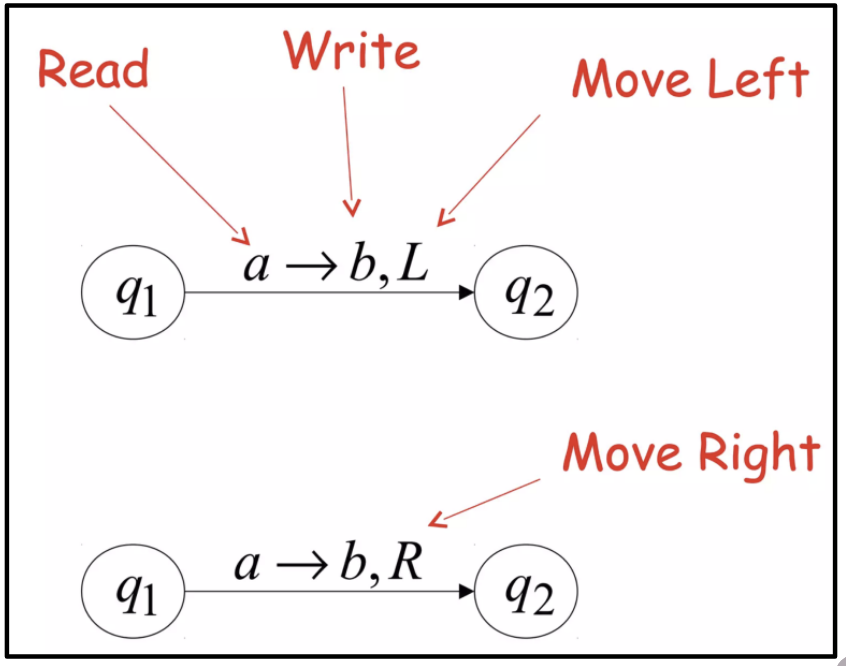
用图来表示图灵机就是:

图灵机示意图

也就是在状态\(q\)下读取纸带上的符号\(a\),然后根据转移函数\(\delta\)转移到状态\(p\),并且对纸带进行操作,要么写入一个符号,要么向左移动,要么向右移动.

一个图灵机识别语言的例子就是

图灵机识别语言示意图

在识别语言\(L=\{a^nb^n|n\geq1\}\)时,图灵机会先扫描纸带上的\(a\),将其替换为\(x\),然后继续向右扫描,直到遇到第一个\(b\),将其替换为\(y\),然后返回纸带的开头,继续扫描下一个\(a\),重复这个过程,直到所有的\(a\)都被替换为\(x\),然后继续扫描纸带,没有可识别的\(a\)了,在识别到\(y\)时就会进入下一个状态,这个状态仅识别\(y\),也就是说此时如果还有多余的\(b\)的话,图灵机就会拒绝输入.

Turing Machine Configuration¶

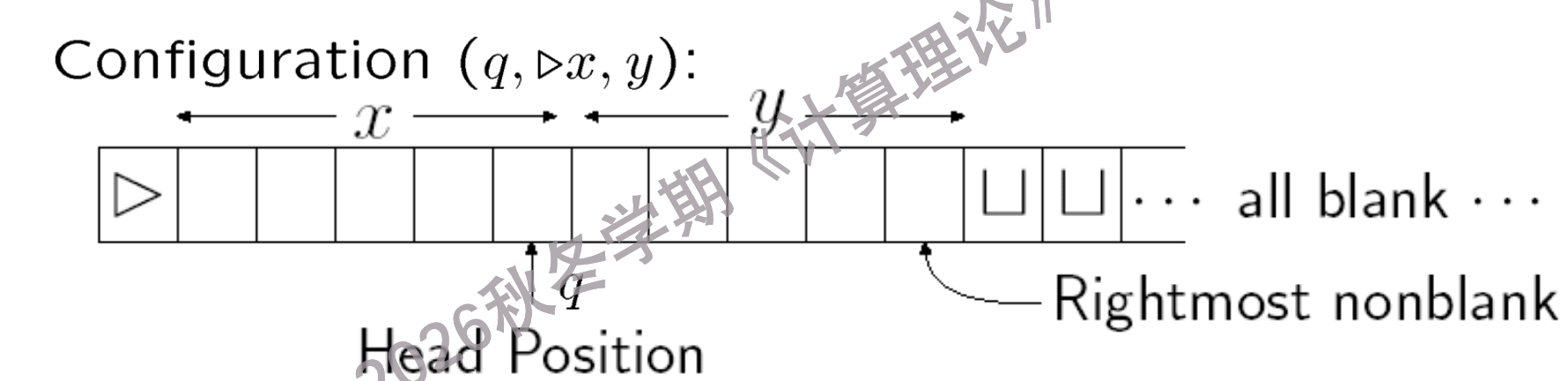
图灵机的配置如下图所示,由其当前的状态与两部分纸带内容组成:

图灵机配置示意图

写作配置\((q,\triangleright x,y)\),其中\(q\)是当前状态,\(x\)是纸带上读头左侧的内容,\(y\)是纸带上读头右侧的内容,一直到最后一个非空白符号为止.

当然,这个配置也可以写成二元组的形式\((q,\triangleright\ \underline{x}y)\),其中\(x\)和\(y\)的定义与上面相同.

更多的例子:

图灵机配置示意图

Computation

设 \(M = (K, \Sigma, \delta, s, H)\) 是一个图灵机，并考虑 \(M\) 的两个配置：\((q_1, w_1\underline{a_1}u_1)\) 和 \((q_2, w_2\underline{a_2}u_2)\)，其中 \(a_1, a_2 \in \Sigma\)。

我们说 \((q_1, w_1\underline{a_1}u_1)\) 在一步之内产生 \((q_2, w_2\underline{a_2}u_2)\)，记作 \((q_1, w_1\underline{a_1}u_1) \vdash_M (q_2, w_2\underline{a_2}u_2)\)，当且仅当，对于某个 \(b \in \Sigma \cup \{\rightarrow, \leftarrow\}\)，有 \(\delta(q_1, a_1) = (q_2, b)\)，并且满足以下三种情况之一：

写入 (Write): \(b \in \Sigma\)
- \(w_1 = w_2\)
- \(u_1 = u2\)
- \(a_2 = b\)
左移 (Move Left): \(b = \leftarrow\)
- \(w_1 = w_2a_2\)
- 并且满足以下任一条件：
  - 如果 \(a_1 \neq \sqcup\) 或 \(u_1 \neq \epsilon\)，则 \(u_2 = a_1u_1\)。例如,\((q_1,xy\underline{a_1}z) \vdash_M (q_2,x\underline{y}a_1z)\)。
  - 如果 \(a_1 = \sqcup\) 且 \(u_1 = \epsilon\)，则 \(u_2 = \epsilon\)。例:如,\((q_1,x\underline{\sqcup}) \vdash_M (q_2,\underline{x})\)。
右移 (Move Right): \(b = \rightarrow\)
- \(w_2 = w_1a_1\)
- 并且满足以下任一条件：
  - 如果 \(a_2 \neq \sqcup\) 或 \(u_2 \neq \epsilon\)，则 \(u_1 = a_2u_2\)。例:\((q_1,xy\underline{a_1}z) \vdash_M (q_2, xya_1\underline{z})\)。
  - 如果 \(a_2 = \sqcup\) 且 \(u_2 = \epsilon\)，则 \(u_1 = \epsilon\)。例:\((q_1,x\underline{a_1}) \vdash_M (q_2,xa_1\underline{\sqcup})\)。

同样,这个推导也有传递和自反闭包.和之前定义的一样,令\(\vdash_M^*\)表示推导的自反传递闭包,\(\vdash_M^n\)表示经过n步推导.

Basic Machine¶

我们将图灵机归结为最简单的两种:Symbol Writing Machine和Hand Moving Machine.

它们的共同特点就是,只做一种操作,要么只写符号,要么只移动读头.只有两种状态.

对于一个固定的字母表 \(\Sigma\) 和一个符号 \(a \in \Sigma \cup \{\leftarrow, \rightarrow\} - \{\triangleright\}\)，我们可以定义一个图灵机 \(M_a = (\{s, h\}, \Sigma, \delta, s, \{h\})\)，其中：

对于每个 \(b \in \Sigma - \{\triangleright\}\)，转移函数为 \(\delta(s, b) = (h, a)\)。
自然地，\(\delta(s, \triangleright) = (s, \rightarrow)\)。

这个图灵机 \(M_a\) 的作用是在读到任何非左端符号后，执行动作 a（写入符号 a、左移或右移），然后立即停机。

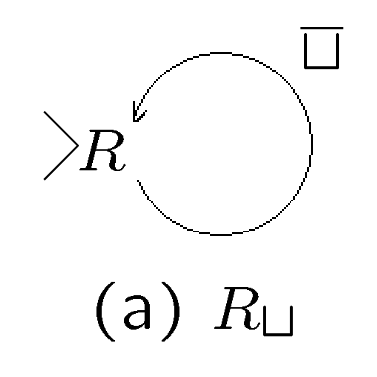
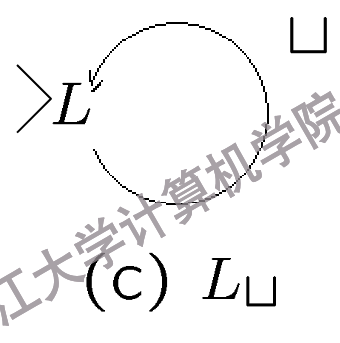
\(R_{\sqcup}\): 找到当前磁带头右侧的第一个空白符号并停机。实现机制是如果读到非空白符号就右移,读到空白符号就停机.

\(R_{\sqcup}\)示意图
\(R_{\bar{\sqcup}}\): 找到当前磁带头右侧的第一个非空白符号并停机。实现机制是如果读到空白符号就右移,读到非空白符号就停机.

\(R_{\bar{\sqcup}}\)示意图
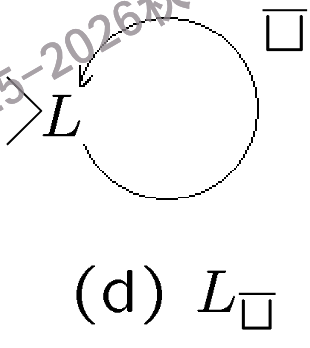
\(L_{\sqcup}\): 找到当前磁带头左侧的第一个空白符号并停机。

\(L_{\sqcup}\)示意图
\(L_{\bar{\sqcup}}\): 找到当前磁带头左侧的第一个非空白符号并停机。

\(L_{\bar{\sqcup}}\)示意图

组合图灵机¶

我们可以将多个图灵机组合成一个更复杂的图灵机，以实现更复杂的功能。例如，我们可以根据纸带上的符号来决定下一个要执行的图灵机。

形式化定义

正式地，令 \(M_i = (K_i, \Sigma, \delta_i, s_i, H_i)\) 为图灵机（其中 \(i = 1, 2, 3\)）。组合后的图灵机为 \(M = (K, \Sigma, \delta, s, H)\)，其中：

\(K = K_1 \cup K_2 \cup K_3\)
\(s = s_1\)
\(H = H_2 \cup H_3\)

对于每个 \(\sigma \in \Sigma\) 和 \(q \in K - H\)，转移函数 \(\delta(q, \sigma)\) 定义如下：

如果 \(q \in K_1 - H_1\)，那么 \(\delta(q, \sigma) = \delta_1(q, \sigma)\)。
如果 \(q \in K_2 - H_2\)，那么 \(\delta(q, \sigma) = \delta_2(q, \sigma)\)。
如果 \(q \in K_3 - H_3\)，那么 \(\delta(q, \sigma) = \delta_3(q, \sigma)\)。
如果 \(q \in H_1\)，那么：
- 若 \(\sigma = a\)，则 \(\delta(q, \sigma) = s_2\)
- 若 \(\sigma = b\)，则 \(\delta(q, \sigma) = s_3\)
- 否则，\(\delta(q, \sigma) \in H\)

形成了如下的结构：

        +-------------------+
        |        M1         |
        |   +-----------+   |
        |   |           |   |
    --> | s1|           |h1 |---+
        |   |           |   |   |
        |   +-----------+   |   |
        +-------------------+   |
              |                 |
           a  |                 | b
              v                 v
        +-------------------+   +-------------------+
        |        M2         |   |        M3         |
        |   +-----------+   |   |   +-----------+   |
        |   |           |   |   |   |           |   |
        | s2|           |h2 |   | s3|           |h3 |
        |   |           |   |   |   |           |   |
        |   +-----------+   |   |   +-----------+   |
        +-------------------+   +-------------------+

箭头表示状态转移的方向。
当 \(M_1\) 运行到 \(h_1\)，根据当前读到的符号（\(a\) 或 \(b\)），分别跳转到 \(M_2\) 或 \(M_3\) 的起始状态继续运行。

使用图灵机¶

图灵机 M 接受输入字符串 \(w \in (\Sigma - \{\sqcup, \triangleleft\})^*\)，如果从初始配置 \((s, \triangleleft\ \underline{\sqcup}w)\) 出发，经过若干步推导后，能够到达一个接受配置

递归函数与递归语言¶

递归函数 (Recursive Functions)

一个函数 \(f\) 被称为是递归的（或可计算的），如果存在一个图灵机 \(M\)，对于任意输入 \(x\)，都能在有限步内停机并输出 \(f(x)\)。

递归语言 (Recursive Languages)

一个语言 \(L\) 被称为是递归的（或可判定的），如果存在一个图灵机 \(M\)，对于任意输入字符串 \(w\)，都能停机并正确地判定 \(w\) 是否属于 \(L\)。具体来说：

如果 \(w \in L\)，则 \(M\) 接受 \(w\)。
如果 \(w \notin L\)，则 \(M\) 拒绝 \(w\)。。

令 \(\Sigma_0 \subseteq \Sigma - \{\sqcup, \triangleleft\}\) 为一个字母表 —— 即 M 的输入字母表。
M 决定 \(L \subseteq \Sigma^*\) 当且仅当对所有 \(w \in \Sigma^*\)，有：
- \(w \in L\) 当且仅当 M 接受 \(w\)；
- \(w \notin L\) 当且仅当 M 拒绝 \(w\)。
如果存在一个图灵机能够判定 \(L\)，则称语言 \(L\) 是递归的（recursive）。

一个例子如下:

图灵机识别语言示意图

这里就用到了我们之前说的基础图灵机

递归可枚举¶

Definition

设 \(M = (K, \Sigma, \delta, s, H)\) 是一个图灵机。令 \(\Sigma_0 \subseteq \Sigma - \{\triangleright, \sqcup\}\) 为一个字母表，\(L \subseteq \Sigma_0^*\)。

半判定 (Semidecide): 图灵机 \(M\) 半判定 \(L\)，当且仅当对所有 \(w \in \Sigma^*\)，以下条件成立：
- \(w \in L\) 当且仅当 \(M\) 在输入 \(w\) 上停机。
递归可枚举 (Recursively Enumerable, r.e.)：一个语言 \(L\) 是递归可枚举的，当且仅当存在一个图灵机 \(M\) 能够半判定 \(L\)

所有递归语言都是递归可枚举语言

递归语言的性质¶

递归语言的补集也是递归语言。
- 只要一个图灵机能够判定语言 \(L\)，我们就可以构造另一个图灵机来判定 \(L\) 的补集 \(\overline{L}\)，方法是交换接受和拒绝状态。
递归语言的并集和交集也是递归语言。
- 对于两个递归语言 \(L_1\) 和 \(L_2\)，我们可以构造一个图灵机来判定它们的并集 \(L_1 \cup L_2\) 和交集 \(L_1 \cap L_2\)，方法是分别运行判定 \(L_1\) 和 \(L_2\) 的图灵机，并根据结果决定接受或拒绝。

其他概念¶

一般的,对于一个输入\(w\),初始状态为\((s,\triangleright\ \underline{\sqcup}w)\),并且\(w\)中不能有\(\triangleright\)和\(\sqcup\)符号.
假设图灵机 \(M\) 在输入 \(w\) 上停机，且 \((s, \triangleright\sqcup w) \vdash_M^* (h, \triangleright\sqcup y)\)，其中 \(y \in \Sigma_0^*\)。则称 \(y\) 为 \(M\) 在输入 \(w\) 上的输出，记作 \(M(w)\)。
计算函数：设 \(f: \Sigma_0^* \to \Sigma_0^*\) 为一个函数。图灵机 \(M\) 计算函数 \(f\)，当且仅当对所有 \(w \in \Sigma_0^*\)，有 \(M(w) = f(w)\)。
递归函数：函数 \(f\) 是递归的，当且仅当存在一个图灵机 \(M\) 能够计算 \(f\)。

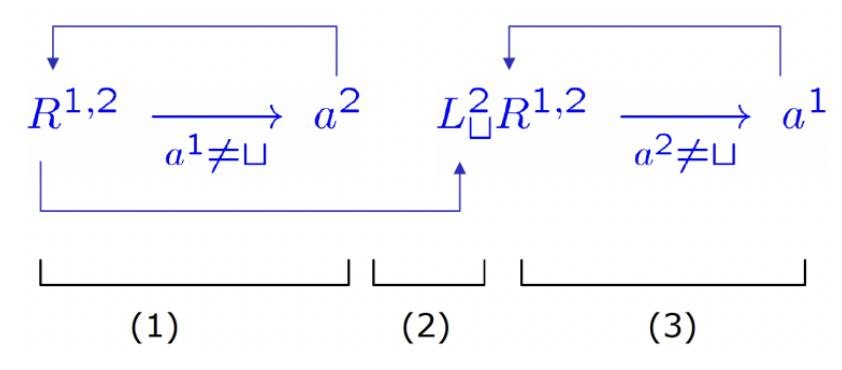
构造一个图灵机计算函数\(succ(n)=n+1\)

图灵机计算函数\(succ(n)=n+1\)示意图

先找到这个二进制串的最后一位,然后:

如果是0,就把它改成1,然后停机.
如果是1,就把它改成0,然后继续向左找下一位,重复这个过程.
如果是空格,说明原来是形如111...1的字符串,就把空格改成1,原来的整体右移一位(已经全部变成0),然后停机.

图灵机拓展¶

Multi-tape Turing Machine¶

k-带图灵机

设 \(k \geq 1\) 是一个整数。\(k\)-带图灵机是一个五元组 \(M = (K, \Sigma, \delta, s, H)\)，其中：

\(K\)、\(\Sigma\)、\(s\) 和 \(H\) 的定义与普通图灵机相同。
转移函数为：\(\delta: (K - H) \times \Sigma^k \to K \times (\Sigma \cup \{\leftarrow, \rightarrow\})^k\)

k-带图灵机的配置

设 \(M = (K, \Sigma, \delta, s, H)\) 是一个 \(k\)-带图灵机。\(M\) 的配置是以下集合的一个成员：

\[K \times \left(\triangleright\Sigma^* \times (\Sigma^* (\Sigma - \sqcup) \cup \{\epsilon\})\right)^k\]

即每一带都有一个左端符号 \(\triangleright\)，左侧的内容，和右侧到最后一个非空白符号的内容。

约定:

输入的字符串被放在第一个磁带上
其他磁带初始时为空白符号,并且头在最左边的空格上
计算的最后,输出在第一个磁带上,其他磁带可以忽略.

复制机 (Copying Machine)

问题：将 \(\sqcup w\sqcup\) 转换为 \(\sqcup w\sqcup w\sqcup\)（其中 \(w\) 不包含空白符号）

解决方案：使用 2-带图灵机实现。

算法步骤：

第一阶段 - 复制到第二带
- 同时向右移动两条磁带的读头
- 将第一条磁带上的每个符号复制到第二条磁带上
- 直到在第一条磁带上遇到空白符号为止
第二阶段 - 准备第二带
- 向左移动第二条磁带的读头
- 直到在第二条磁带上遇到空白符号为止
第三阶段 - 复制回第一带
- 同时向右移动两条磁带的读头
- 将第二条磁带上的符号复制到第一条磁带上
- 当第二条磁带上遇到空白符号时停机

结果：第一条磁带最终包含 \(\sqcup w\sqcup w\sqcup\)

复制机示意图

一个例子

Two-way Infinite Tape¶

定义: 纸带向左和向右都是无限延伸的。
约定: 输入/输出约定与标准图灵机相同。
结论: 拥有双向无限纸带的图灵机并不比标准图灵机更强大。
证明思路: 一个双向无限纸带可以很容易地被一个 2-带图灵机 模拟。
- 比如，可以将双向无限纸带从某个位置“折叠”，用一条带子存储右半部分，另一条带子存储左半部分。

Multiple Heads¶

定义: 一个多头图灵机只有一条纸带，但有多个读写头。
操作: 在一步操作中，所有的头同时感测扫描到的符号，并独立地进行移动或写入。
结论: 多头图灵机可以很容易地被 k-带图灵机 模拟。
模拟思路:
1. 分轨 (Tracks): 将纸带分成多个轨道，其中除了一条轨道用于存储数据外，其余轨道仅用于记录读写头的位置。
2. 两遍扫描 (Two-pass Scan): 为了模拟多头图灵机的一步操作，必须扫描纸带两次：
  - 第一次: 找到所有读写头位置上的符号。
  - 第二次: 根据规则更改这些符号或适当地移动读写头。

直观理解: 为什么必须跑两趟? from Gemini

这就好比一个指挥官 (单头) 要指挥分布在战线不同位置的多个士兵 (多头) 同时行动。

因为指挥官没有“上帝视角”，他不能同时看到所有士兵的情况，所以必须分两步走：

第一趟 (收集情报): 指挥官必须先从头走到尾，记下每个士兵当前看到了什么敌人（读取符号）。只有跑完全程，他才能掌握全局信息，决定下一步的战术。
第二趟 (传达命令): 战术制定好后（状态转移），指挥官必须再从头走到尾，告诉每个士兵该怎么做（改写符号或移动位置）。

这就是为什么单头模拟多头时，每一步操作都需要来回跑两趟的原因。

Non-deterministic Turing Machine¶

非确定性图灵机 (NTM)

非确定性图灵机 (NTM) 是一个五元组 \(M = (K, \Sigma, \Delta, s, H)\)，其中 \(K, \Sigma, s, H\) 与标准图灵机定义相同，但 \(\Delta\) 是以下集合的一个子集：

\[ (K - H) \times \Sigma \times K \times (\Sigma \cup \{\leftarrow, \rightarrow\}) \]

这意味着 \(\Delta\) 是一个关系 (relation)，而不是一个函数。

配置与推导: 配置以及关系 \(\vdash_M\) 和 \(\vdash_M^*\) 的定义与标准图灵机类似。
非确定性: \(\vdash_M\) 不必是单值的。也就是说，一个配置在一步操作中可能会产生多个不同的后续配置。

NTM 的语言识别与计算¶

由于非确定性图灵机 (NTM) 的计算路径像一棵树，我们对“接受”、“判定”和“计算”的定义需要特别注意路径的存在性和全路径的有限性。

1. 半判定 (Semidecide)

我们说 NTM \(M\) 半判定 语言 \(L\)，如果对于所有输入 \(w\)：

\[ w \in L \iff M \text{ 接受 } w \]

接受 (Accept): 只要存在至少一条计算路径能到达停机状态，就叫接受。
也就是说: 只要运气够好，能猜对一条路走通，就算赢。不管其他路是不是死循环。

2. 判定 (Decide)

我们说 NTM \(M\) 判定语言 \(L\)，如果满足两个条件：

全路径有限 (Bounded Depth): 对于任何输入 \(w\)，存在一个自然数 \(N\)（取决于 \(M\) 和 \(w\)），使得没有配置的推导步数超过 \(N\)。
- 这意味着所有计算路径都必须在有限步内停机，不存在死循环。
正确性: \(w \in L \iff M \text{ 接受 } w\)。
- 即：如果是 \(L\) 中的string，总有一条路能停在接受状态 \(y\)。
也就是说:
- 首先，这台机器绝不能死循环。无论怎么猜，最后都得停下来给个结果。
- 其次，如果是接受的string，总能找到一种走法说“Yes”。
- 如果是拒绝的string，所有走法最后都会停在拒绝状态 \(h\)。

3. 计算函数 (Compute a Function)

我们说 NTM \(M\) 计算函数 \(f\)，如果满足：

全路径有限: 同样要求不存在死循环，所有路径长度有限。
输出一致性: \(M\) 停机并输出 \(v \iff v = f(w)\)。
也就是说:
- 首先，不能死循环。
- 其次，所有停下来的路径，输出结果必须完全一样，都是 \(f(w)\)。
- 不能有的路算出 1，有的路算出 2。大家殊途同归。

NTM 半判定合数集合

任务: 设计一个 NTM 半判定集合 \(C = \{ \text{num}(p \cdot q) : p, q \geq 2 \}\) (即合数集合)。

思路: 利用 NTM 的“猜测”能力，直接猜两个因子 \(p\) 和 \(q\)，然后验证它们的乘积是否等于输入。

算法步骤:

猜测 (Guess): 非确定性地选择两个二进制数 \(p\) 和 \(q\) (均大于 1)，并将它们写在输入 \(n\) 的旁边。
- 注: 这里体现了 NTM 的强大之处，它不需要遍历所有可能的因子，而是直接“猜”出一对。
验证 (Verify): 调用乘法图灵机，计算 \(p \cdot q\)。
比较 (Check): 比较计算出的 \(p \cdot q\) 与原输入 \(n\) 是否相等。
- 如果相等: 停机 (Halt)。这意味着猜对了，\(n\) 确实是一个合数，机器接受。
- 如果不相等: 进入死循环 (Loop forever)。这意味着这条猜测路径失败了。

结果:

如果 \(n\) 是合数，一定存在某对 \(p, q\) 使得 \(p \cdot q = n\)。NTM 会有一条路径猜中这对因子并停机，所以 \(M\) 接受 \(n\)。
如果 \(n\) 是质数，无论怎么猜，\(p \cdot q\) 都不可能等于 \(n\)。所有路径都会进入死循环，所以 \(M\) 不接受 \(n\)。
这符合半判定的定义：合数能停机，质数永远停不下来。

Theorem: NTM \(\equiv\) DTM¶

定理: 对于任何非确定性图灵机 (NTM) \(M\)，都存在一个确定性图灵机 (DTM) \(M'\)，使得 \(L(M) = L(M')\)。即 NTM 和 DTM 在计算能力上是等价的。

证明思路: NTM 的计算过程可以看作一棵计算树 (Computation Tree)，树的每个节点是一个配置，根节点是初始配置。因为 NTM 可能会死循环（树的深度无限），我们不能简单地用深度优先搜索 (DFS)，必须使用 广度优先搜索 (BFS) 来系统地遍历这棵树。

构造方法: 我们可以构造一个 3-带 DTM \(M'\) 来模拟 NTM \(M\)。

磁带结构:
- 带 1 (Input): 始终存储原始输入 \(w\)，只读。
- 带 2 (Simulation): 用于模拟 NTM \(M\) 在某条特定路径上的计算过程（工作带）。
- 带 3 (Address): 存储当前要尝试的路径地址（即计算树上的节点路径）。
地址编码:
- 设 \(M\) 的最大分支数（即一步操作中最多有多少种选择）为 \(b\)。
- 我们可以用一个 \(b\) 进制的数字序列来表示计算树上的一条路径。例如序列 1-3-2 表示：第1步选第1种转移，第2步选第3种转移，第3步选第2种转移。
模拟过程: \(M'\) 按字典序（长度递增）生成带 3 上的地址序列（\(\epsilon, 1, 2, ..., b, 11, 12, ...\)），对每个序列执行以下操作：
1. 初始化: 将带 1 的输入 \(w\) 复制到带 2，重置模拟状态。
2. 运行: 在带 2 上模拟 \(M\) 的运行。每一步转移时，读取带 3 上的下一个数字，决定选择哪一种转移。
3. 判断:
  - 接受: 如果 \(M\) 进入了接受状态，则 \(M'\) 停机并接受。
  - 中止: 如果带 3 的数字序列用完了但 \(M\) 还没停机，或者序列对应的选择无效（比如该状态只有2种转移但序列写了3），则中止当前模拟，清空带 2，准备尝试带 3 的下一个序列。
  - 拒绝: 如果 \(M\) 进入拒绝状态，同样中止当前模拟。

结论:

如果 \(M\) 接受 \(w\)，说明计算树上存在至少一个接受节点。由于 BFS 会按层遍历树的所有节点，\(M'\) 最终一定会找到这个接受节点并停机接受。
如果 \(M\) 不接受 \(w\)，说明计算树上没有接受节点。\(M'\) 会一直运行下去（模拟所有可能的路径），这与 NTM 的半判定行为（死循环）一致。
因此，\(L(M) = L(M')\)。

Grammars¶

文法 (Grammar)

一个文法（或无限制文法 Unrestricted Grammar）是一个四元组 \(G = (V, \Sigma, R, S)\)，其中：

\(V\) 是一个字母表 (Alphabet)。
\(\Sigma \subseteq V\) 是终结符 (Terminal symbols) 的集合。\(V - \Sigma\) 被称为非终结符 (Nonterminal symbols) 的集合。
\(S \in V - \Sigma\) 是起始符号 (Start symbol)。
\(R\) 是规则 (Rules) 的集合，它是 \(V^* (V - \Sigma) V^* \times V^*\) 的一个有限子集。
- 也就是说，规则的形式为 \(\alpha \to \beta\)，其中 \(\alpha\) 必须包含至少一个非终结符。

推导 (Derivation):
- 我们说 \(u \Rightarrow_G v\)，如果 \(u = x\alpha y, v = x\beta y\)，且 \(\alpha \to \beta \in R\)。
- \(\Rightarrow_G^*\) 是 \(\Rightarrow_G\) 的自反传递闭包。
语言 (Language):
- 文法 \(G\) 生成的语言是 \(L(G) = \{ w \in \Sigma^* : S \Rightarrow_G^* w \}\)。
- 也就是说，从起始符号 \(S\) 开始，经过有限步推导，最终生成的全终结符字符串的集合。

实际上,Grammar产生的语言和NTM接受的语言是一样的。

Numerical Functions¶

原始递归函数 (Primitive Recursive Functions)¶

原始递归函数是由基本函数通过组合和原始递归操作构成的函数类。

基本函数 (Basic Functions)¶

基本函数

基本函数包含以下三类：

零函数 (Zero Function): 对于任意 \(k \ge 0\)，\(k\) 元零函数定义为 \(zero_k(n_1, \dots, n_k) = 0\)。
- 通常简记为 \(Z(n) = 0\)。
后继函数 (Successor Function): 定义为 \(succ(n) = n + 1\)。
- 通常简记为 \(S(n) = n + 1\)。
投影函数 (Projection Functions / Identity Functions): 对于 \(k \ge j > 0\)，第 \(j\) 个 \(k\) 元投影函数定义为 \(id_{k,j}(n_1, \dots, n_k) = n_j\)。
- 通常记为 \(P_j^k(x_1, \dots, x_k) = x_j\)。

构造复杂函数¶

通过以下两种操作，我们可以从基本函数构建出更复杂的函数：

组合 (Composition)

组合 (Composition)

对于 \(k, l \ge 0\)，设 \(g: \mathbb{N}^k \to \mathbb{N}\) 是一个 \(k\) 元函数，\(h_1, \dots, h_k\) 是 \(l\) 元函数。

那么 \(g\) 与 \(h_1, \dots, h_k\) 的组合是一个 \(l\) 元函数 \(f\)，定义为：

\[ f(n_1, \dots, n_l) = g(h_1(n_1, \dots, n_l), \dots, h_k(n_1, \dots, n_l)) \]
原始递归 (Primitive Recursion)

原始递归 (Primitive Recursion)

对于 \(k \ge 0\)，设 \(g\) 是一个 \(k\) 元函数，\(h\) 是一个 \((k+2)\) 元函数。

由 \(g\) 和 \(h\) 定义的函数 \(f\) 是一个 \((k+1)\) 元函数，定义如下：

\[ \begin{aligned} f(n_1, \dots, n_k, 0) &= g(n_1, \dots, n_k) \\ f(n_1, \dots, n_k, m+1) &= h(n_1, \dots, n_k, m, f(n_1, \dots, n_k, m)) \end{aligned} \]

对于所有 \(n_1, \dots, n_k, m \in \mathbb{N}\)。

原始递归谓词 (Primitive Recursive Predicates)¶

原始递归谓词 (Primitive Recursive Predicate)

原始递归谓词是一个只取值 0 和 1 的原始递归函数。

原始递归谓词示例

以下谓词是原始递归的：

iszero(n):
- 如果 \(n = 0\)，则为 1。
- 如果 \(n > 0\)，则为 0。
- 递归定义：
  - \(iszero(0) = 1\)
  - \(iszero(m + 1) = 0\)
positive(n):
- 定义为 \(sgn(n)\)。
greater-than-or-equal(m, n) (\(m \ge n\)):
- 定义为 \(iszero(n \dot{-} m)\)
- (其中 \(n \dot{-} m\) 表示真减法/Monus：如果 \(n \ge m\) 则为 \(n-m\)，否则为 0)
less-than(m, n):
- 定义为 \(1 \dot{-} greater\text{-}than\text{-}or\text{-}equal(m, n)\)

原始递归谓词的取反，合取与析取结果都是原始递归函数

原始递归函数集是可枚举的。
- 每个原始递归函数原则上都可以用有限字母表上的字符串来表示。
- 该字母表应包含用于表示恒等函数、后继函数和零函数的符号，用于表示原始递归和组合的符号，以及括号和用于二进制基本函数索引的符号 0 和 1。
- 我们可以枚举该字母表上的所有字符串，并保留那些是原始递归函数合法定义的字符串。

事实上,原始递归函数是递归函数的真子集。

最小化 (Minimalization)¶

原始递归函数的一个限制是它们总是全函数 (Total Functions)（即对所有输入都有定义且停机）。为了捕获所有可计算函数（包括那些可能死循环的偏函数），我们需要引入最小化操作。

最小化 (Minimalization / Unbounded Search)

对于 \(k \ge 0\)，设 \(g\) 是一个 \((k+1)\) 元函数。

由 \(g\) 的最小化定义的函数 \(f\) 记作 \(f(n_1, \dots, n_k) = \mu m [g(n_1, \dots, n_k, m) = 1]\)。

\(f(n_1, \dots, n_k)\) 的值是满足以下条件的最小自然数 \(m\)：

\(g(n_1, \dots, n_k, m) = 1\)；
对于所有 \(m' < m\)，\(g(n_1, \dots, n_k, m')\) 都有定义且 \(g(n_1, \dots, n_k, m') \neq 1\)。

注意：如果对于给定的输入，不存在这样的 \(m\)，或者在找到满足条件的 \(m\) 之前，计算某个 \(g(n_1, \dots, n_k, m')\) 时未定义（死循环），那么 \(f(n_1, \dots, n_k)\) 未定义。

相当于执行:

m = 0
while True:
    result = g(x, m)   # 1. 尝试计算 g(x, m)
    if result == 1:    # 2. 判定是否满足条件
        return m       # 3. 找到了！停机并返回 m
    m = m + 1          # 4. 没找到，试下一个

一个函数 \(g\) 被称为是可最小化的，如果上述寻找 \(m\) 的过程总是能停机（即总能找到解）。

具体来说，一个 \((k+1)\) 元函数 \(g\) 是可最小化的，如果它满足以下性质：

\[ \forall n_1, \dots, n_k \in \mathbb{N}, \exists m \in \mathbb{N} \text{ such that } g(n_1, \dots, n_k, m) = 1 \]

感性的说,原始递归函数相当于一个for循环,是有限的;而最小化操作相当于一个while循环,是无限的。

例子：对数函数 (Logarithm Function)

利用最小化，我们可以定义对数函数：

\[ \log(m, n) = \lceil \log_{m+2}(n + 1) \rceil = \mu p [\text{greater-than-or-equal}((m + 2) \uparrow p, n + 1)] \]

这里使用 \(m+2\) 和 \(n+1\) 是为了避免 \(m \le 1\) 或 \(n=0\) 时的定义域错误
这是一个恰当的 \(\mu\)-递归函数定义，因为函数 \(g(m, n, p) = \text{greater-than-or-equal}((m + 2) \uparrow p, n + 1)\) 是可最小化的（即对于任意 \(m, n\)，总存在足够大的 \(p\) 使得 \((m+2)^p \ge n+1\)）。

\(\mu\)-递归函数 (\(\mu\)-Recursive Functions)¶

\(\mu\)-递归函数

一个函数被称为 \(\mu\)-递归函数，如果它可以从基本函数出发，通过有限次的组合、原始递归和对可最小化函数的最小化操作获得。

\(\mu\)-递归函数\(\leftrightarrow\)图灵机可计算函数¶

定理: 一个函数是 \(\mu\)-递归的，当且仅当它是图灵机可计算的。

太复杂了...