索引¶

约 1936 个字 4 行代码 25 张图片预计阅读时间 10 分钟

Basic Concepts¶

索引是一个数据结构，用于加速对数据库表中数据的访问。
Search Key: 索引的关键字，用于查找数据。
一个Index File包含多个Index Entry，每个Index Entry包含一个Search Key和一个指向数据记录的指针。

Search Key Record Pointer
有两种索引类型:
- Ordered Index: 索引条目按顺序排列，适用于范围查询。
- Hash Index: 索引条目无序排列，适用于等值查询。

Index Evaluation Metrics¶

索引的评估指标

Access types supported efficiently. E.g.,
- Point query: records with a specified value in the attribute,点查询
- Range query: or records with an attribute value falling in a specified range of values,范围查询
Access time
Insertion time
Deletion time
Space overhead

Ordered Indices¶

Indexes that are ordered by the search key.

有如下的概念:

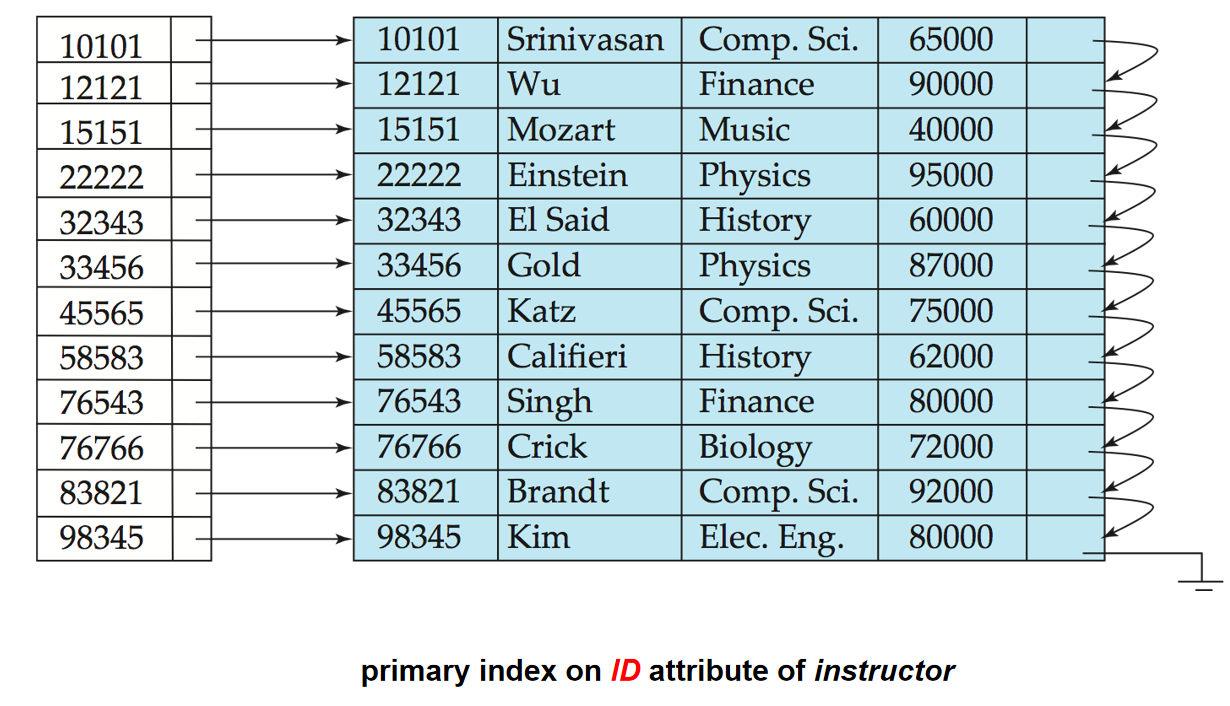
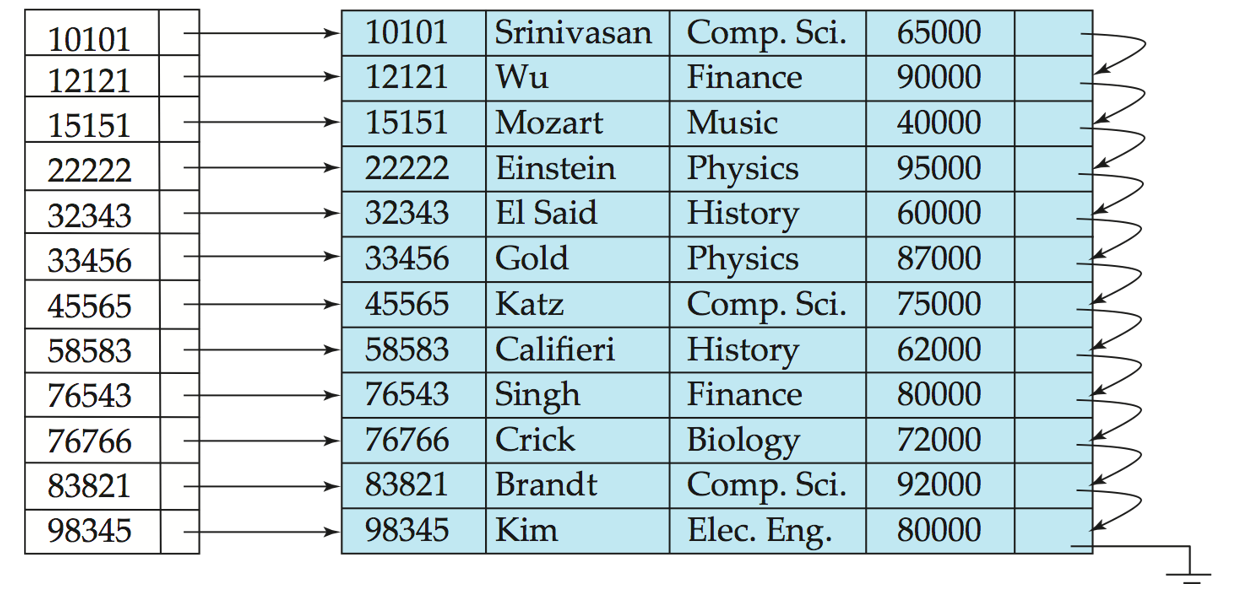
Primary Index(主索引): 也称为clustering index（聚集索引）.决定了排列顺序的索引,其Search Key通常,但并不一定,是主键.主索引的记录在文件中是有序的.
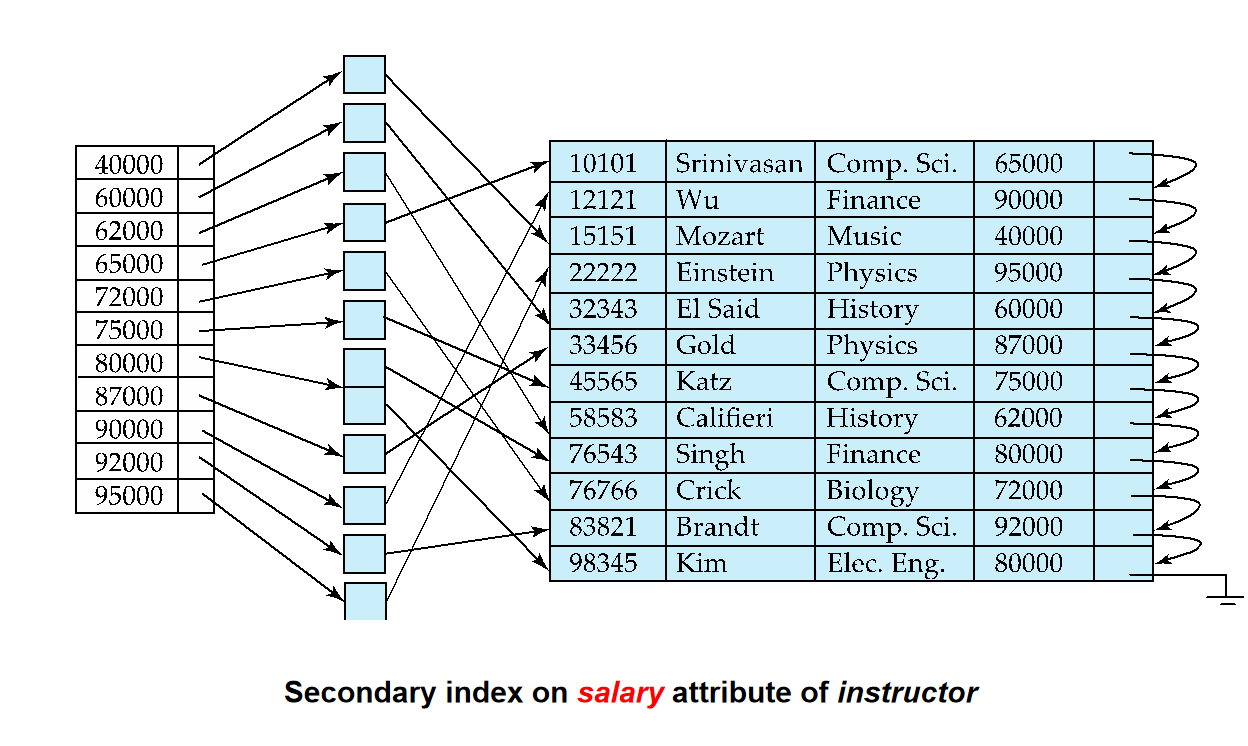
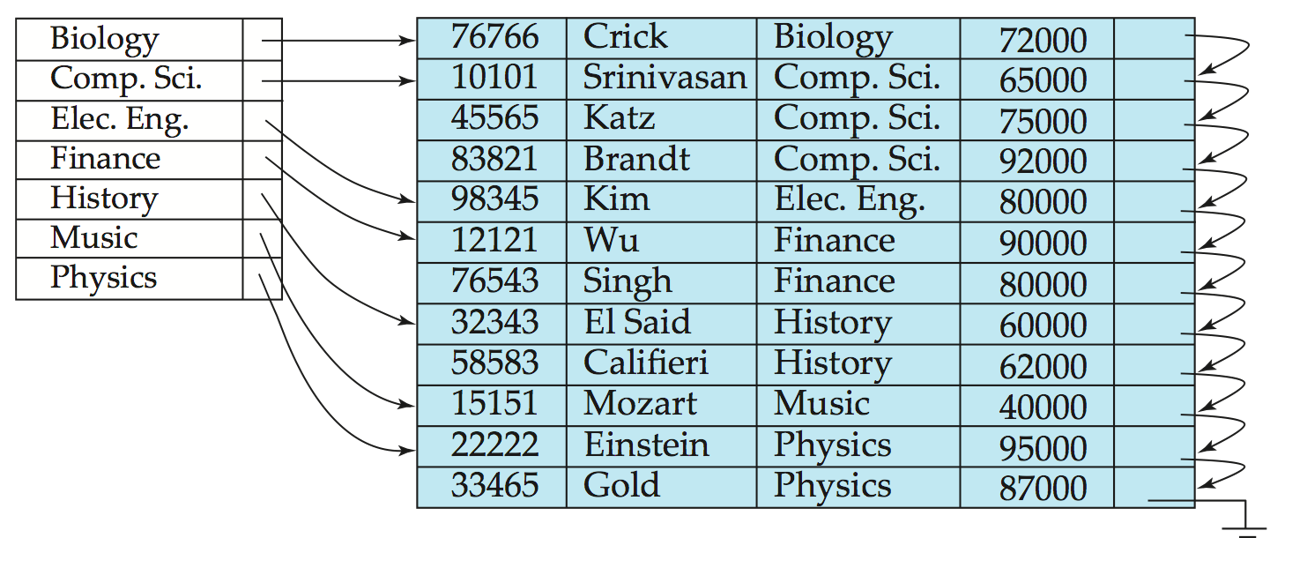
Secondary Index(次索引): 也称为non-clustering index（非聚集索引）.它决定的顺序与文件实际排列的顺序不一样.
Index-sequential file（索引顺序文件）: ordered sequential file with a primary index.
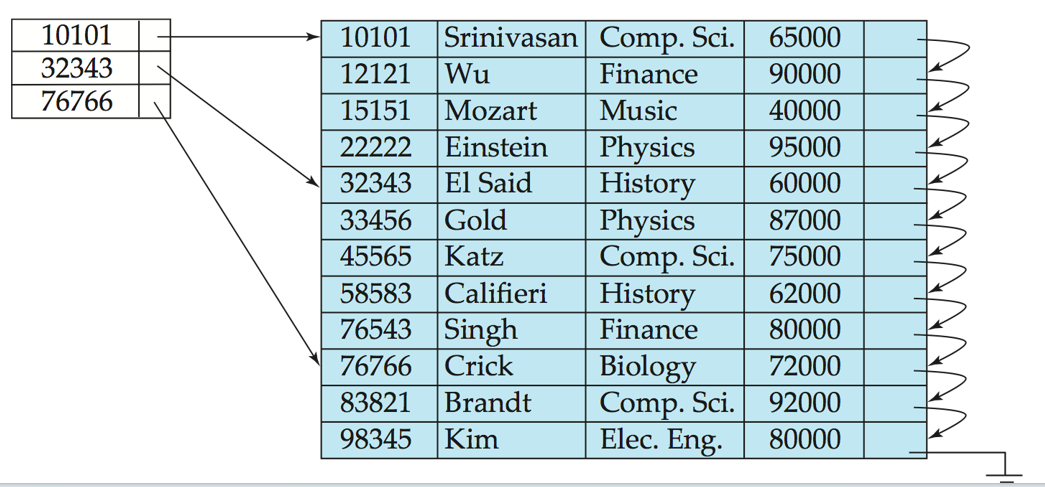
Dense Index Files(稠密索引文件): 所有的Search Key都有一个索引条目.每个索引条目都指向一个数据记录.

稠密索引

稀疏索引

Sparse Index Files(稀疏索引文件): 只有一部分Search Key有索引条目.每个索引条目都指向一个数据块.
- Good tradeoff: sparse index with an index entry for every block in file, corresponding to least search-key value in the block.
- 和B+树有点像.

Multilevel Index (多级索引)¶

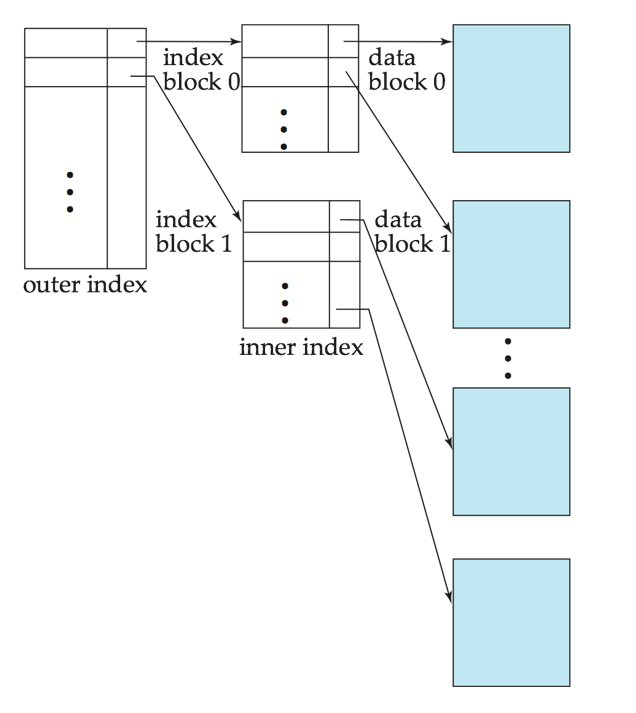
Treat primary index kept on disk as a sequential file and construct a sparse index on it.
- outer index – a sparse index of primary index
- inner index – the primary index file

B+-Tree Index¶

和ADS一样

一个B+树节点典型的结构如下:

\(K_i\)是搜索键的值.通常\(K_1<K_2<...<K_{n-1}\)
\(P_i\)是指向下一个节点的指针.如果是叶子节点,那么\(P_i\)指向数据记录.如果是非叶子节点,那么\(P_i\)指向下一个节点.
对于叶子节点,\(P_n\)指向下一个叶子节点,也就是下一个数据记录.

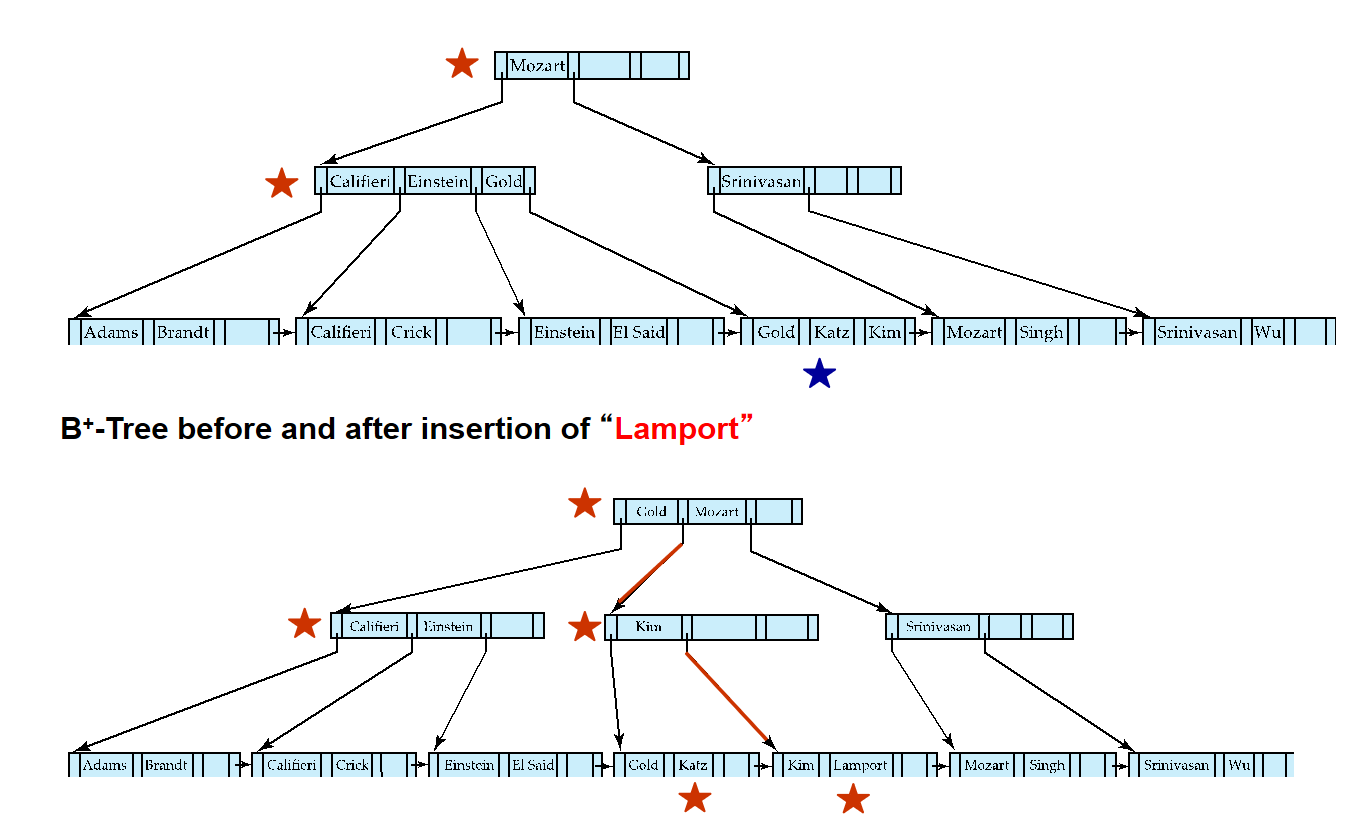
Examples¶

由于ADS中已经学过相关操作,所以这里就放一些B+树的例子.

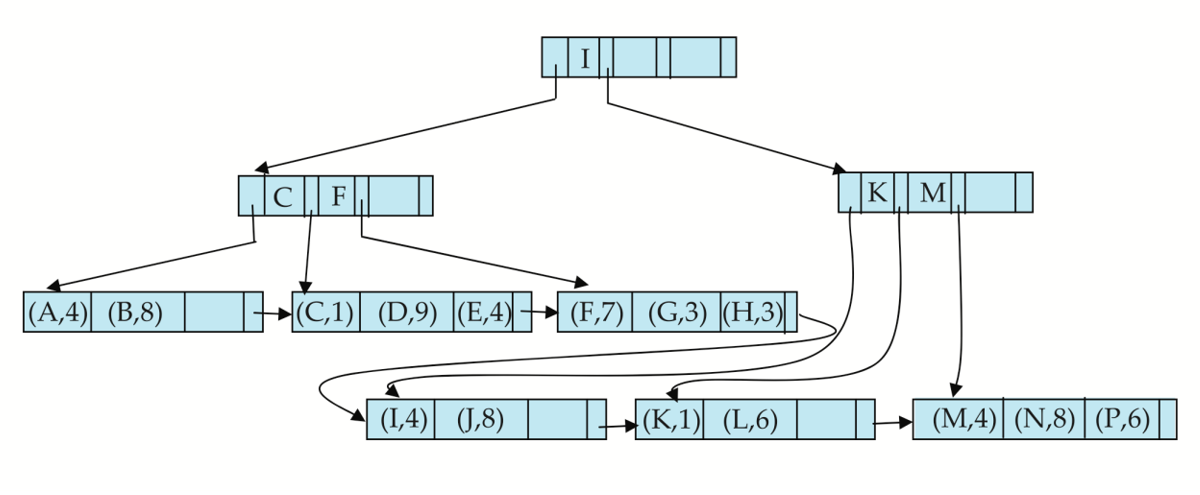
B+ Tree¶

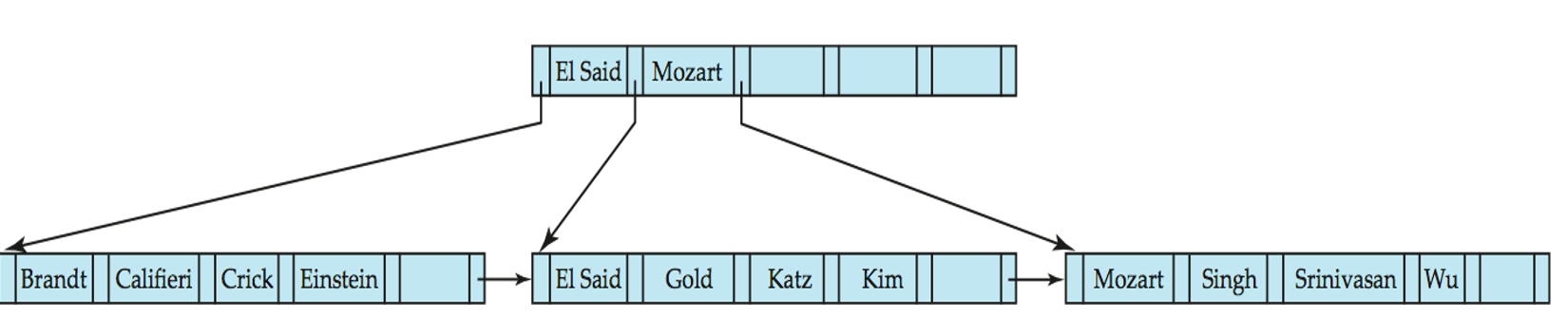
对于下图的B+树:

其阶数n=6
叶子节点的键值数目范围是[3,5] 这里和ADS不一样,是[(n-1)/2,n-1]
非叶子节点的孩子数目范围是[3,6]
根节点要么是叶子,要么至少有两个孩子

高度结论

如果一个B+树中存储了\(K\)个索引,则其高度的范围是:

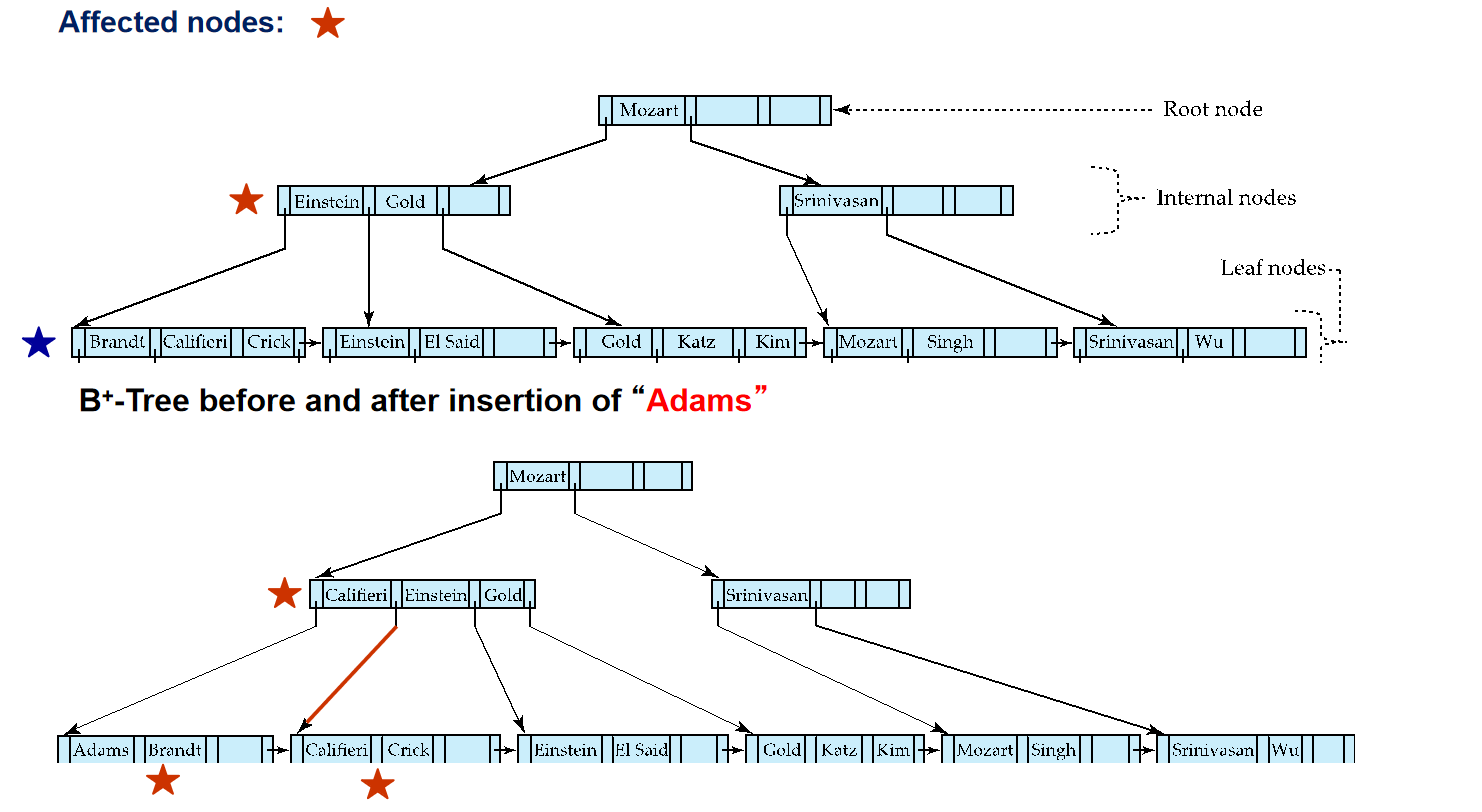
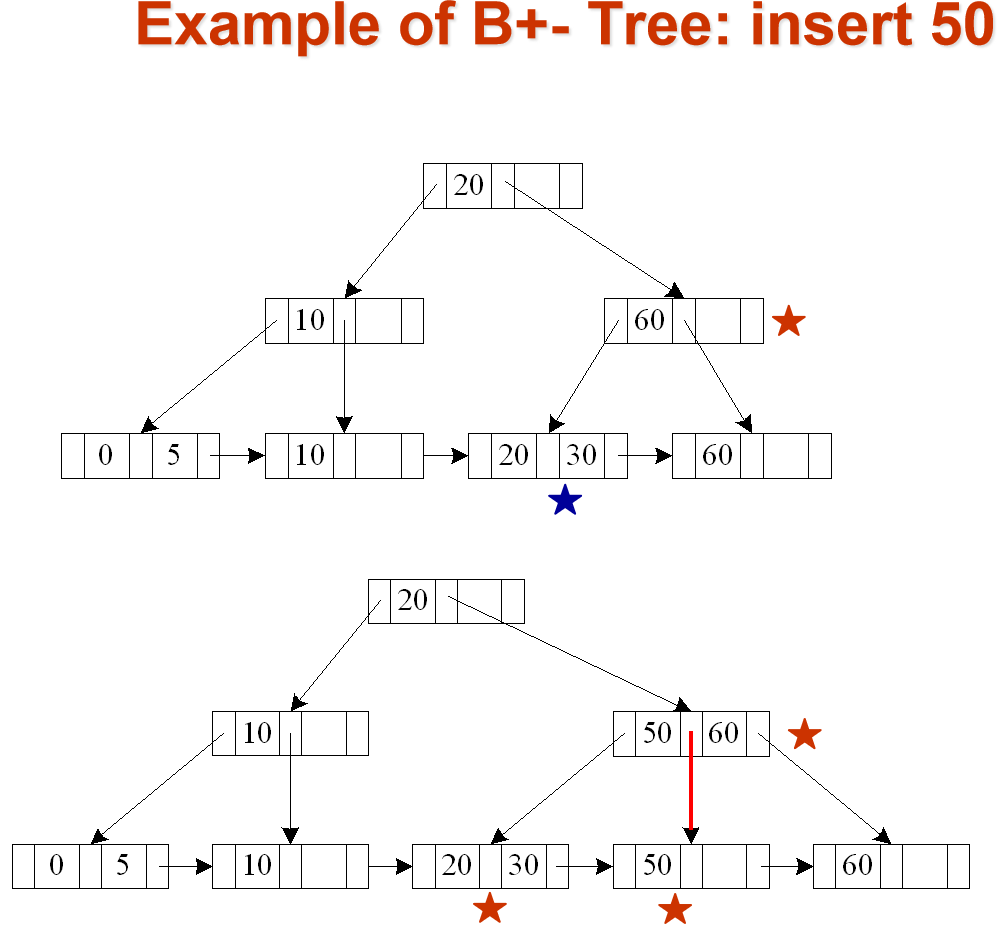
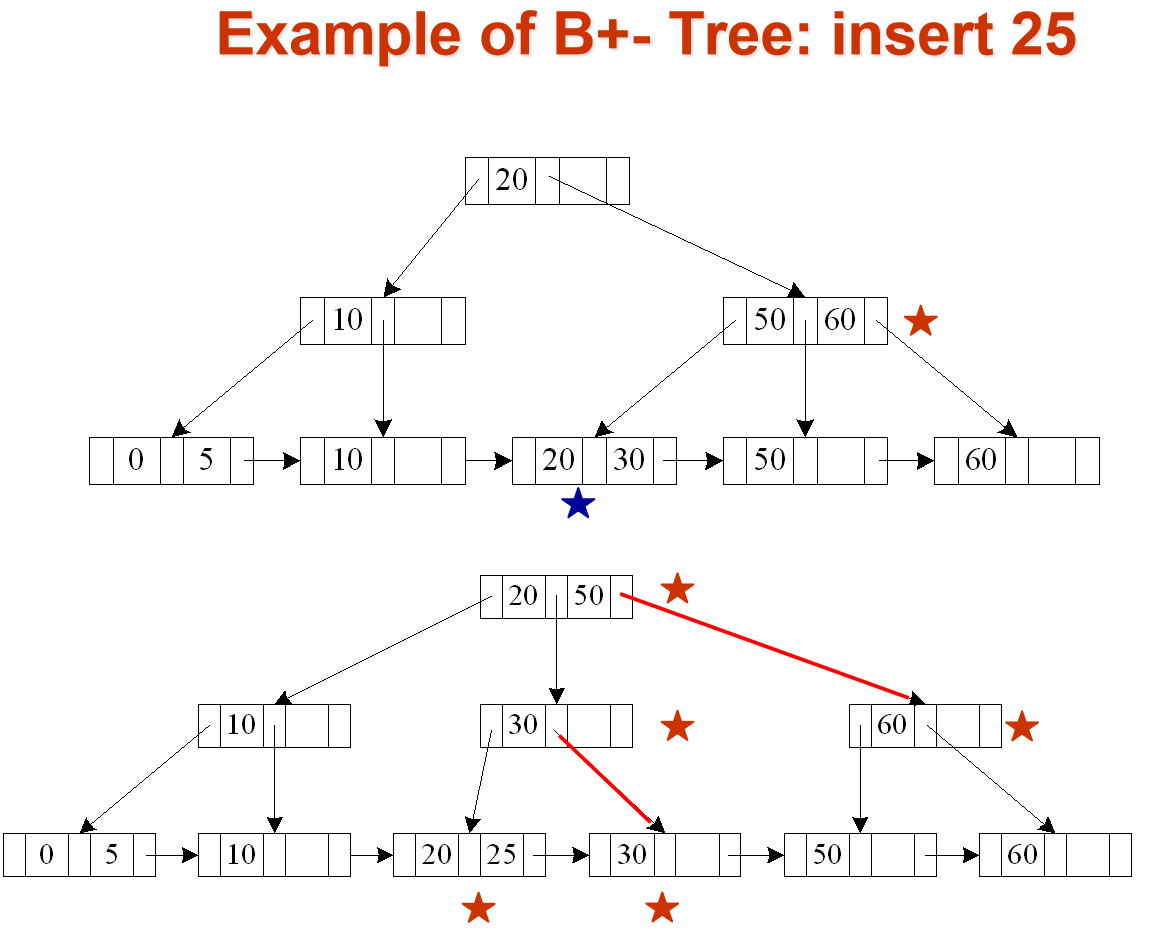
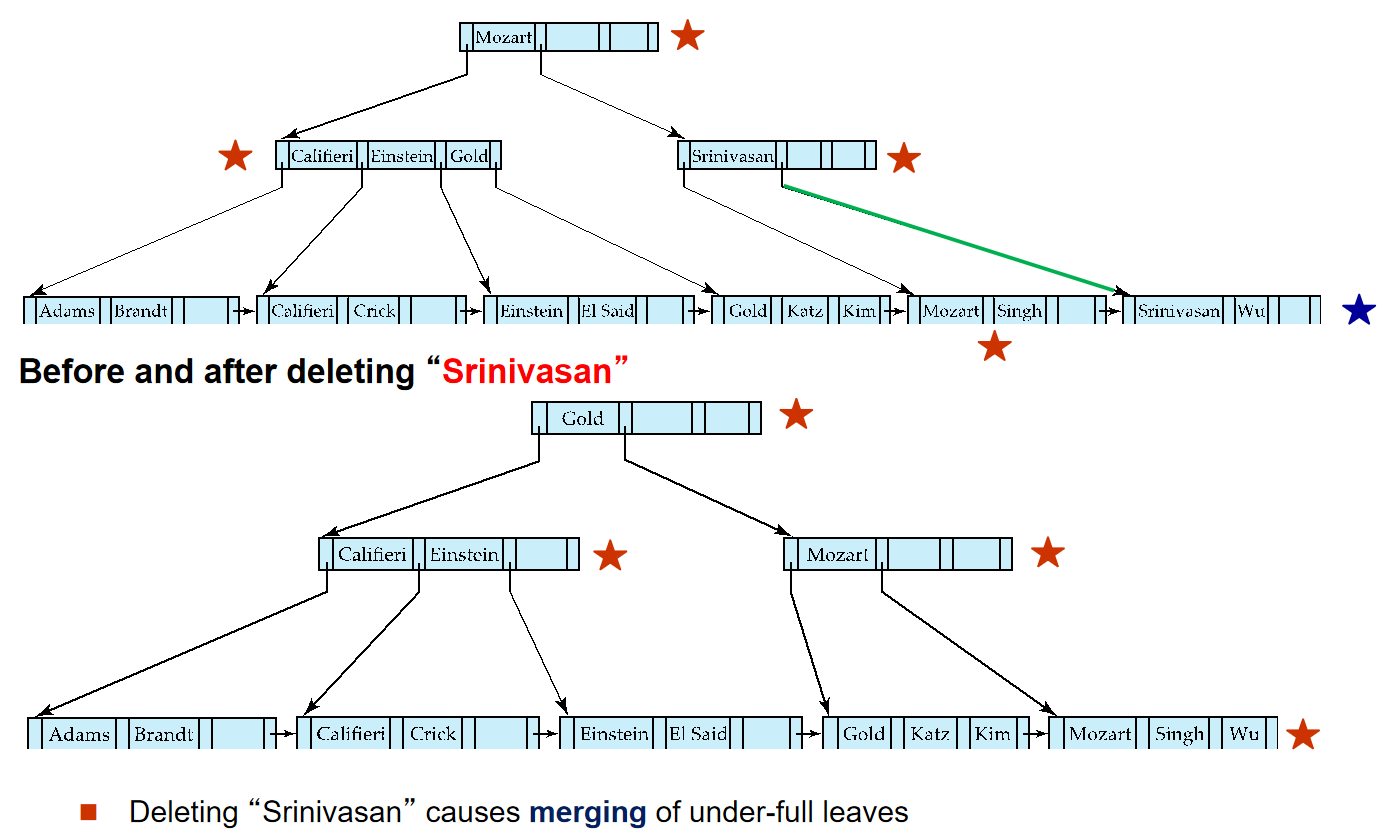
\[ max{\lceil \log_{n/2} {K/2} \rceil +1 ,\lceil \log_{n/2} K \rceil }\geq h \geq \lceil \log_{n} K \rceil \]

插入与删除¶

所有的例子

Average node occupancy depends on insertion order

\(\frac{2}{3}\) with random, \(\frac{1}{2}\)with insertion in sorted order

B+- tree : height and size estimation¶

对于如下的数据定义:

person( pid char(18)  primary key，
        name char(8),   
        age smallint,                             
        address char(40) );

与1000000个人相关的记录.

一个block大小4KB,一个指针大小4B,一个char(18)大小18B,一个char(8)大小8B,一个smallint大小2B,一个char(40)大小40B.

因此一个block可以存储的记录数为:

\[ \frac{4096}{8+18+2+40}=\frac{4096}{68}\approx 60 \]

B+树的阶数为:

\[ \frac{4096-4}{18+4}+1=\frac{4092}{22}+1\approx 187 \]

如果是两层的B+树,那么最多可以存储的记录数为:

\[ 187*186\approx 34782 \]

如果是三层的B+树,那么最多可以存储的记录数为:

\[ 187*187*186\approx 6504234 \]

因此我们使用三层的B+树,可以存储下上面这一百万条记录.

一个叶子可以存储[93,186]条记录,一个非叶子节点可以有[94,187]个孩子

半满叶节点情况

节点层级计算值向上取整单位

叶节点数 10752.69 10752 nodes

第二层节点数 114 114 nodes

根节点 1 1 node

总节点数(最多) 10867 10867 nodes
满叶节点情况

节点层级计算值向上取整单位

叶节点数 5376.344 5377 nodes

第二层节点数 29 29 nodes

根节点 1 1 node

总节点数(最小) 5407 5407 nodes

B+ Tree File Organization¶

B+-Tree File Organization:
- Leaf nodes in a B+-tree file organization store records, instead of pointers.存储记录而不是指针
- Helps keep data records clustered even when there are insertions/deletions/updates
Leaf nodes are still required to be half full
- Since records are larger than pointers, the maximum number of records that can be stored in a leaf node is less than the number of pointers in a nonleaf node.

Other Issues in Indexing¶

Record relocation and secondary indices
- If a record is relocated, all secondary indices on the record must be updated.
- 这会导致节点的分裂开销十分大
- 解决方法是:在二级索引中不要直接存储记录地址，而是存储该记录的“主键”值，再通过主索引定位记录。
Variable length strings as keys
- Variable fanout
Prefix compression
- Keys in leaf node can be compressed by sharing common prefixes
- Keep enough characters to distinguish entries in the subtrees separated by the key value
  - E.g. “Silas” and “Silberschatz” can be separated by “Silb”

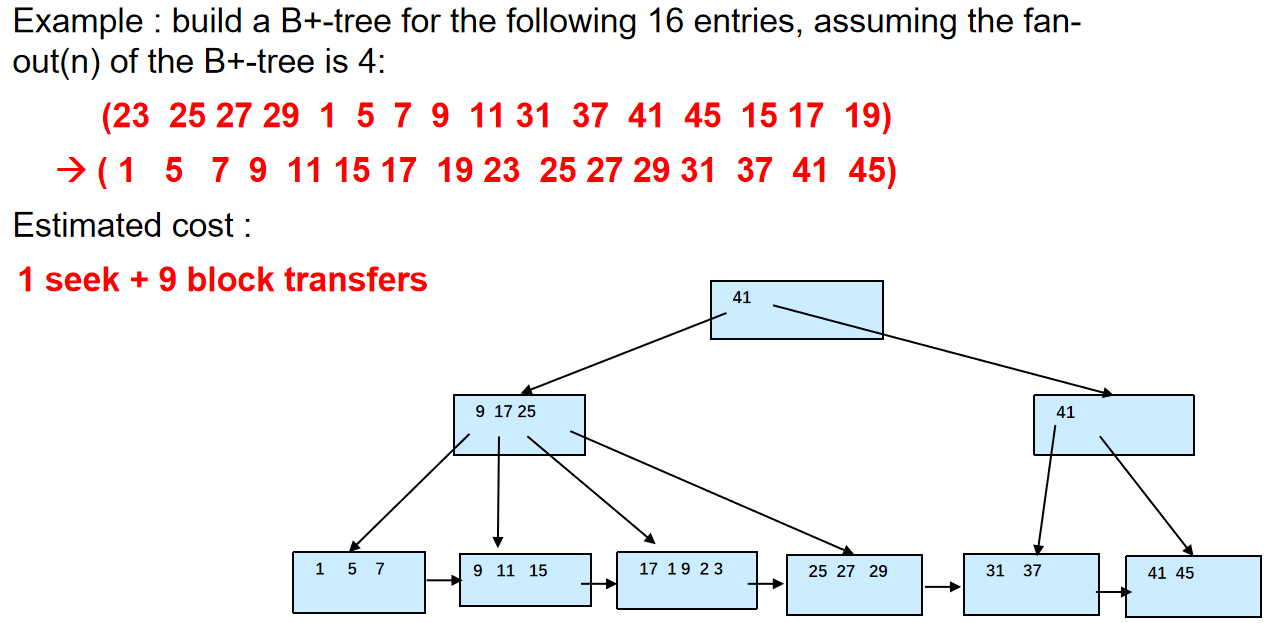
Bulk Loading and Bottom-Up Build¶

批量加载和自底向上构建

Inserting entries one-at-a-time into a B+-tree requires  1 IO per entry

因此,我们有两种解决方法:

Insert in sorted order
- 充分利用数据局部性.
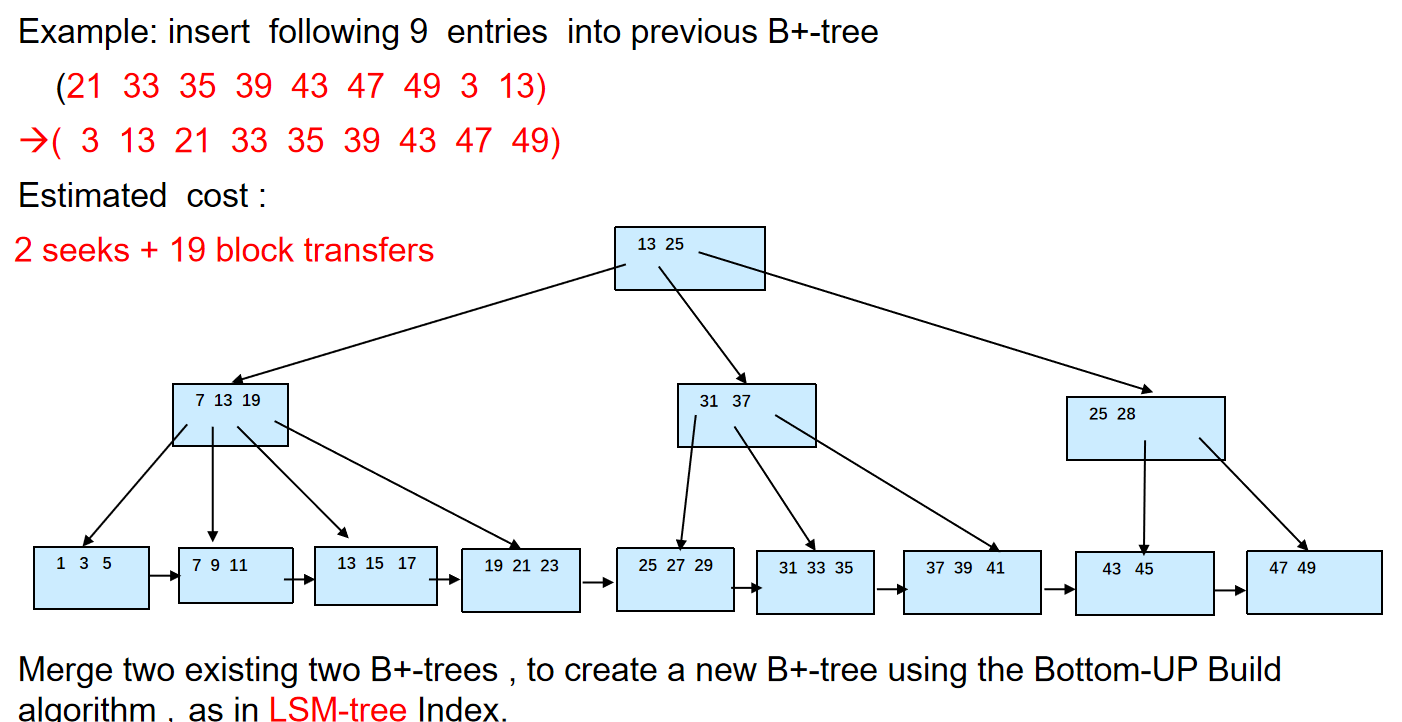
Bottom-up B+-tree construction
- 和上面一样,先排序
- 然后从底部开始构建B+-树

Bulk Loading

Bulk insert index entries¶

Bulk Insert

先把之前那颗树的叶子节点找到,1 Seek+6 blocks

然后构建完树后,把树再写回去,1 Seek+13 blocks

Multiple-Key Access¶

Composite search keys are search keys containing more than one attribute
- E.g. (dept_name, salary)
Lexicographic ordering: (a1, a2) < (b1, b2) if either
- a1 < b1, or
- a1=b1 and a2 < b2

Indexing in Main Memory¶

当索引结构（如 B+ 树）主要或完全存储在主内存（RAM）中时，我们需要考虑新的性能优化点。

内存访问的成本：
- 虽然内存随机访问比磁盘/闪存快得多，但与 CPU 缓存（Cache）相比，仍然相对较慢且存在延迟。
大节点与缓存未命中（Cache Misses）：
- 传统 B+ 树为优化磁盘 I/O 而设计的大节点，在内存中进行内部查找（如二分查找）时，容易跨越多个block，导致频繁的缓存未命中，降低效率。
缓存友好（Cache-Conscious）数据结构：
- 对于内存索引，优化重点转向最大化 CPU 缓存利用率。我们需要设计“缓存友好”的数据结构。

关键思想（Key Idea）：

为了平衡磁盘/内存访问和缓存访问的优化：

保留大节点： 继续使用较大的 B+ 树节点，以减少磁盘 I/O（如果需要）或整体内存访问（如减少 TLB 未命中）。
优化节点内部结构： 不再使用简单的有序数组，而是在大节点内部嵌入一个小的、缓存友好的树结构（例如，节点大小与缓存行匹配的小 B 树）。这样，节点内部的查找操作能更好地利用缓存，减少未命中。

Indexing on Flash¶

在闪存中，写入不是立即的，需要等待原来的数据被擦除后才能写入新的数据。

闪存的随机读取速度远快于磁盘，没有寻道和旋转延迟。因此，读取小页面和大页面的延迟差异远小于磁盘

并且，如果使用大页面，擦除时的代价就会很高。

Optimum page size therefore much smaller
Bulk-loading still useful since it minimizes page erases
Write-optimized tree structures (i.e., LSM-tree) have been adapted to minimize page writes for flash-optimized search trees

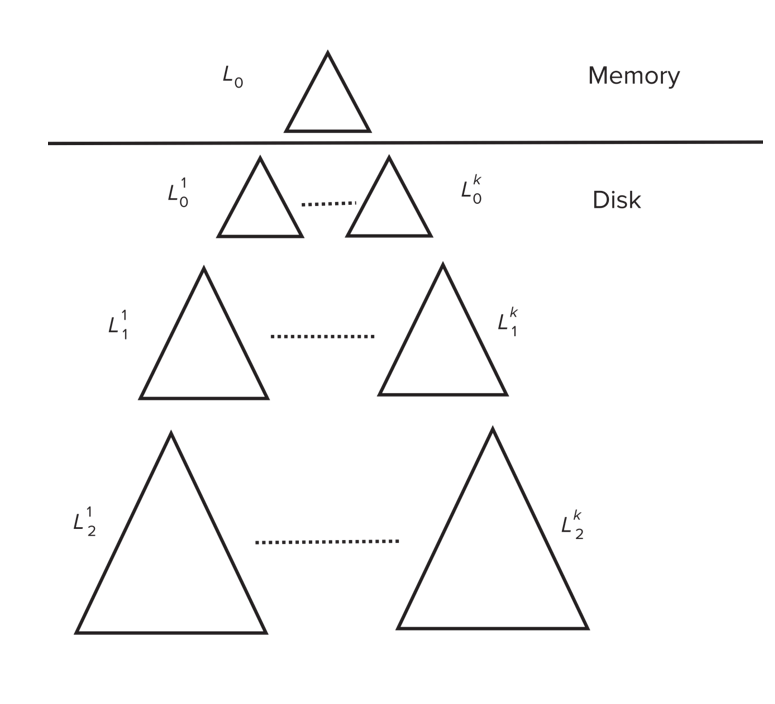
Log Structured Merge (LSM) Tree¶

LSM Tree

LSM树是一种数据结构，旨在优化写入操作的性能。它通过将写入操作首先存储在内存中，然后定期将这些数据批量写入磁盘，从而减少随机写入的次数。

插入数据时:

数据块先插入到内存中的\(L_0\)树
当\(L_0\)树满了，使用bottom-up build的策略把\(L_0\)树中的数据写入到\(L_1\)树中
当\(L_1\)树的大小超过某个阈值，就把它合并到\(L_2\)树中
以此类推，有\(L_3\)树，\(L_4\)树，...

Stepped Merge Index¶

当一层上存在k个索引时，把它们合并为下一层的一个树。

布隆过滤器可以用来快速判断一个元素是否在某个集合中。

使用一个位数组和多个哈希函数。
添加元素时，用哈希函数计算多个位置，并将这些位置的位设为 1。
查询元素时，检查其哈希函数对应的所有位：
- 如果所有位都是 1，则报告元素可能存在。
- 如果至少有一位是 0，则报告元素绝对不存在。

Delete¶

在LSM树中，如果我们要删除一个entry,我们就加入一个特殊的delete entry，然后：

在查询时，同时查找original entry和delete entry,如果有entry和某个delete entry匹配了，就不返回
在合并树时，如果我们找到某个delete entry匹配了某个entry,就把这个这两个entry都删除掉

Buffer Tree¶

Key idea: each internal node of B+-tree has a buffer to store inserts

也就是把B+树每个节点剩下的空间用来存储插入的记录. - 这样可以减少磁盘I/O,因为我们可以把插入的记录先存储在内存中,等到节点满了再写入磁盘.

Bitmap Indices¶

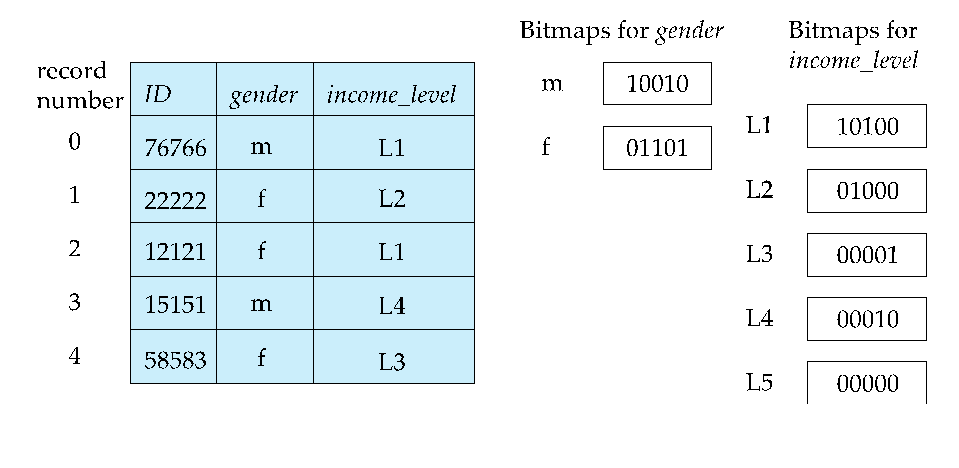
认为一个关系里的一个个元组都是从0开始有序依次编号的

对于每一个属性的每一种值，都有一个bitmap，1表示该元组的该属性为这个值,反之为0.

因此,bitmap使用于那些值比较少的属性,比如性别,国家,城市等.

Bitmap Indices

Bitmap Indices对于多值属性的查找非常友好,只要把两个属性值的bitmap做与(and)/或(or)操作就可以了.

Bitmaps are packed into words": 位图在内存中不是按单个位存储的，而是被打包成 CPU 的原生字长（Word Size），通常是 32 位或 64 位。这意味着一个 32 位的整数可以存储位图中的 32 个连续位。
为了快速知道结果位图中有多少个 1,我们使用如下方法
1. 预计算数组: 事先创建一个包含 256 个元素的数组（我们称之为 popcount_lookup）。数组的索引范围是 0 到 255，正好对应一个字节（8 位）能表示的所有可能值。
2. 数组内容: popcount_lookup[i] 存储的是整数 i 的二进制表示中包含的 1 的个数。例如：
  - popcount_lookup[0] (二进制 00000000) = 0,
  - popcount_lookup[1] (00000001) = 1,
  - popcount_lookup[2] (00000010) = 1,
  - popcount_lookup[3] (00000011) = 2,
  - ...,
  - popcount_lookup[255] (11111111) = 8
3. 将位图按字节（8 位）拆分。对于每个字节，直接以该字节的值作为索引去查预计算数组，就能立刻得到这个字节中 1 的个数。

节点层级	计算值	向上取整	单位
叶节点数	10752.69	10752	nodes
第二层节点数	114	114	nodes
根节点	1	1	node
总节点数(最多)	10867	10867	nodes

节点层级	计算值	向上取整	单位
叶节点数	5376.344	5377	nodes
第二层节点数	29	29	nodes
根节点	1	1	node
总节点数(最小)	5407	5407	nodes

索引¶