Chapter 2:关系数据模型¶
约 2472 个字 15 张图片 预计阅读时间 12 分钟
关系数据模型
正如我们在第一章中所讨论的那样,关系数据模型是一种用于表示数据的结构化方法。在关系数据模型中,数据被组织为表格(表)的形式。表格是由行和列组成的,其中每行代表一个实体,每列代表一个属性。表格中的每个单元格包含一个值。
关系数据库是基于关系数据模型的数据库。
关系¶
给定集合 \(D_1, D_2, \dots, D_n\),一个关系 \(r\) 是 \(D_1 \times D_2 \times \dots \times D_n\) 的子集。因此,一个关系是由 \(n\) 元组 \((a_1, a_2, \dots, a_n)\) 所组成的集合,其中每个 \(a_i \in D_i\)。
而所谓 Relation Schema, 是关系的模式,它定义了关系的名称以及每个属性的名称和类型。例如:
instructor = {name, dept_name, salary}
而关系实例可以是:
r = { (Wu, Finance, 90000),
(Mozart, Music, 40000),
(Gold, Physics, 87000),
(Singh, Finance, 80000) }
Keys¶
在关系模型中,一个关键(Key)是一个属性或属性集合,它可以唯一标识一个元组。
Superkey(超键)¶
一个超键是一个属性集合,它可以唯一标识一个元组。例如,{name}不是一个超键,因为存在同名的人,但是{name,ID}的组合是一个超键。
Candidate Key(候选键)¶
一个候选键是一个最小的超键,即它是一个超键,但是去掉任何一个属性后就不再是超键。例如,{ID}是一个候选键,但是{ID, name}不是。
Primary Key(主键)¶
一个主键是一个候选键,且没有任何冗余属性。{ID}是一个主键,而{ID, name}不是。一般主键属性要加下划线,即{ID, name} -> {ID, name}。
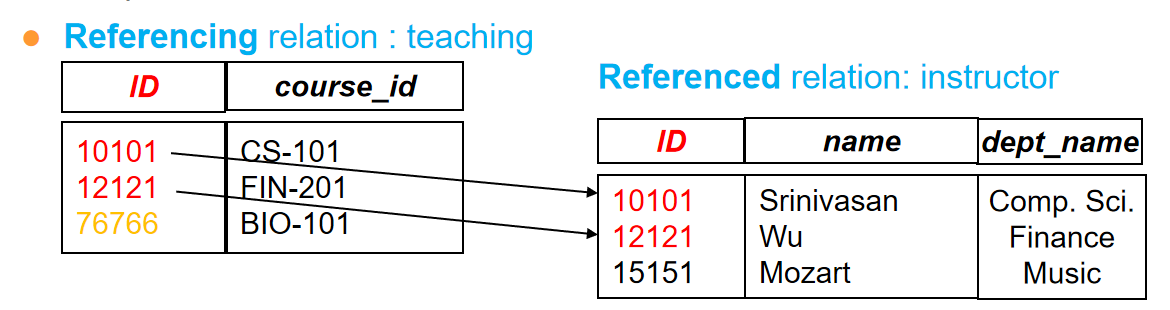
Foreign Key(外键)¶
外键就是一张表里某一列属性,它的值都可以在另一张表的主键中找到。个人感觉与C语言的指针有点像,指向另一张表的主键。
外键需要参照完整性(Referential integrity)约束,即外键的值必须在被参照的表的主键中存在。
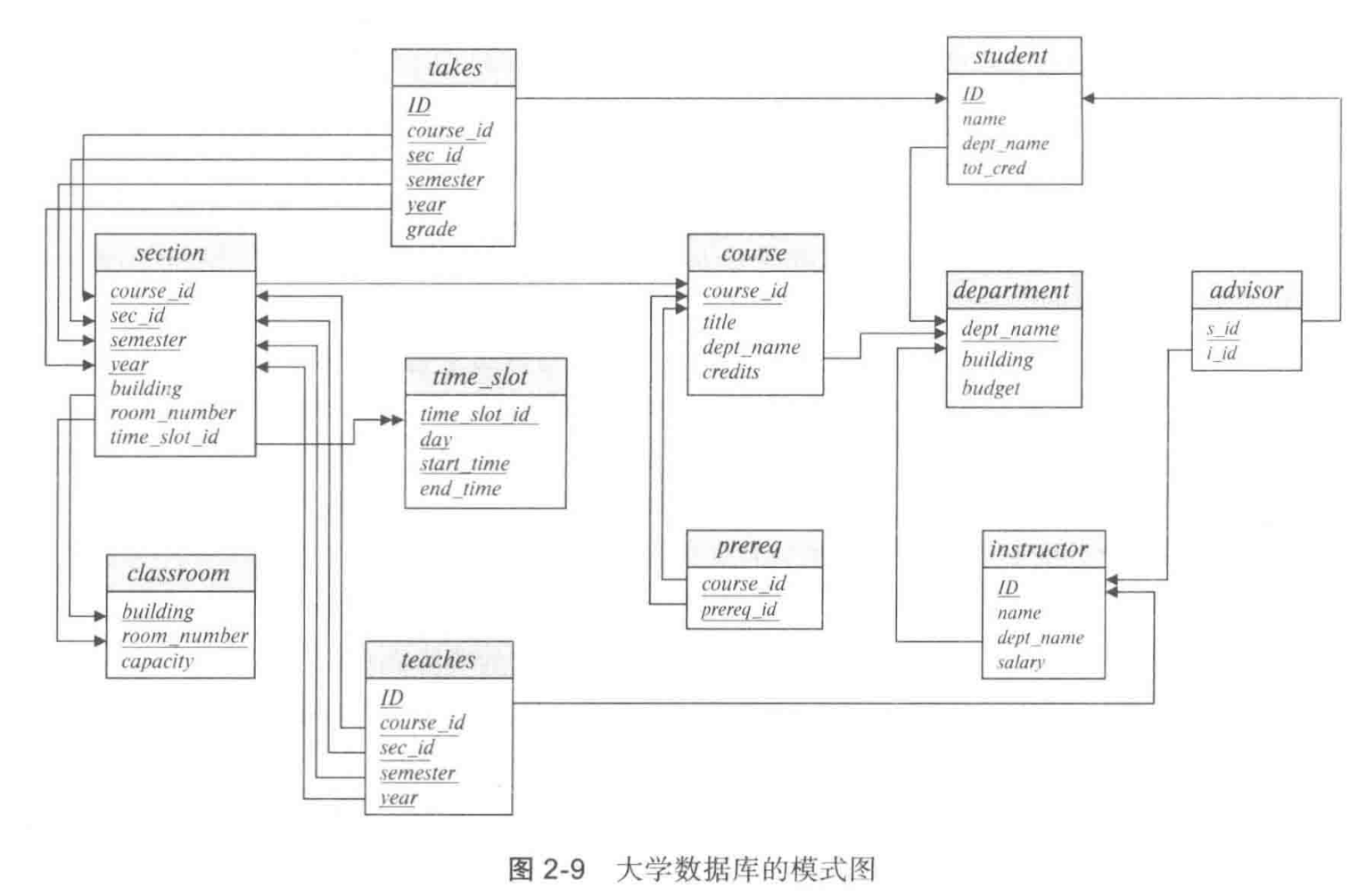
模式图¶
有了主键与外键的概念,我们可以画出模式图。例如:
关系查询语言¶
关系查询语言是用于查询数据库的语言,它可以分为两类:
-
关系代数:关系代数是一种形式化的查询语言,它使用一组操作来操作关系。这些操作包括选择、投影、连接、并、差、交等。
-
关系演算:关系演算是一种声明性的查询语言,它描述了所需的数据,而不是如何获取数据。关系演算分为两种:元组关系演算和域关系演算。
上面两类语言在计算上是等价的,即可以相互转换。
六类基本操作¶
我们一般使用关系代数来查询数据库,分为如下六类:
Select:\(\sigma\)¶
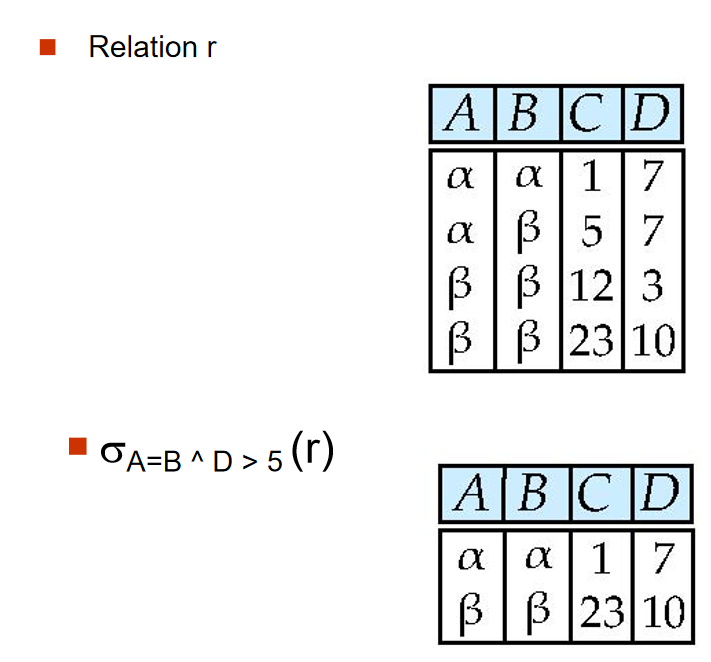
选择操作,选择满足条件的元组。表示为\(\sigma_{condition}(relation)\)。condition是由属性,常量和逻辑运算符(和离散数学一样,使用 \(\lor\), \(\land\), \(\lnot\))组成的条件。例如:\(\sigma_{dept_name='Finance'}(instructor)\), 选择出dept_name为Finance的元组;\(\sigma_{salary>80000}(instructor)\), 选择出salary大于80000的元组。
Project:\(\Pi\)¶
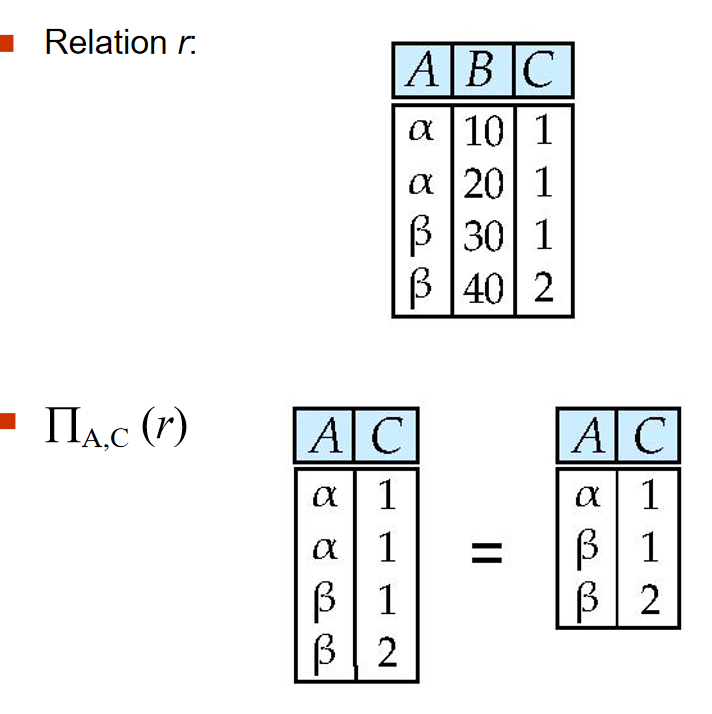
投影操作,选择满足条件的属性。表示为\(\Pi_{attribute}(relation)\)。例如:\(\Pi_{name, dept_name}(instructor)\), 选择出name和dept_name属性,组成一个新的关系。
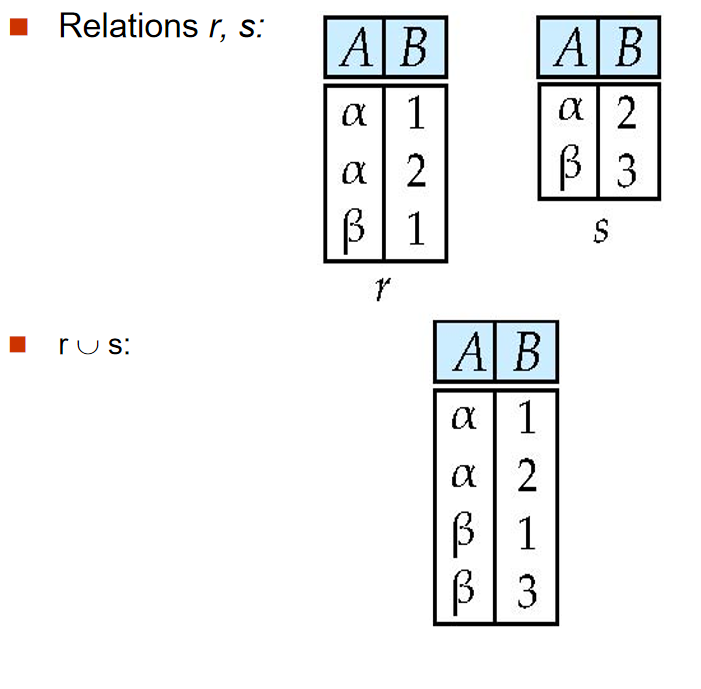
Union:\(\cup\)¶
并操作,合并两个关系。被合并的两个关系必须满足如下条件:
-
两个关系的属性数目(arity)相同。
-
属性的域(domain)是兼容的。
例如,要找到所以2009年秋学期与2010年春学期的课,可以这样写:
\(\Pi_{course_id}(\sigma_{semester='Fall' \land year=2009}(section)) \cup \Pi_{course_id}(\sigma_{semester='Spring' \land year=2010}(section))\)
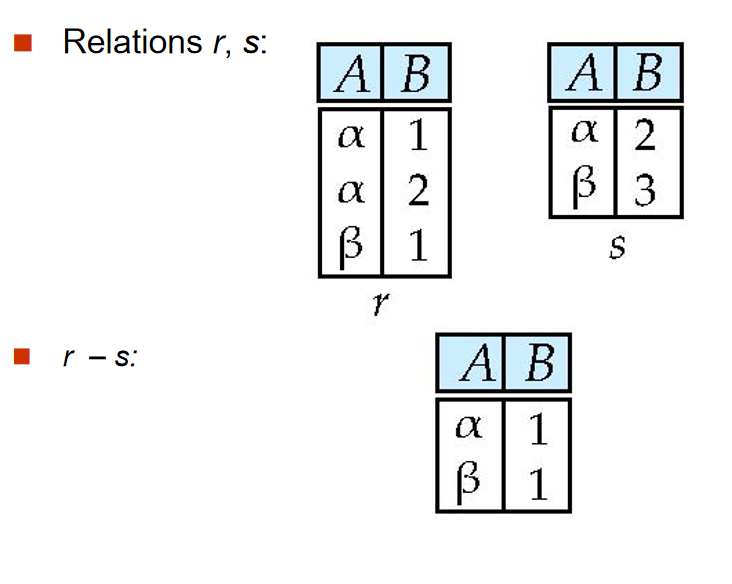
Set Difference:\(-\)¶
差操作,返回两个关系的差集。
例如,要找到所有2009年秋学期但不是2010年春学期的课,可以这样写:
\(\Pi_{course_id}(\sigma_{semester='Fall' \land year=2009}(section)) - \Pi_{course_id}(\sigma_{semester='Spring' \land year=2010}(section))\)
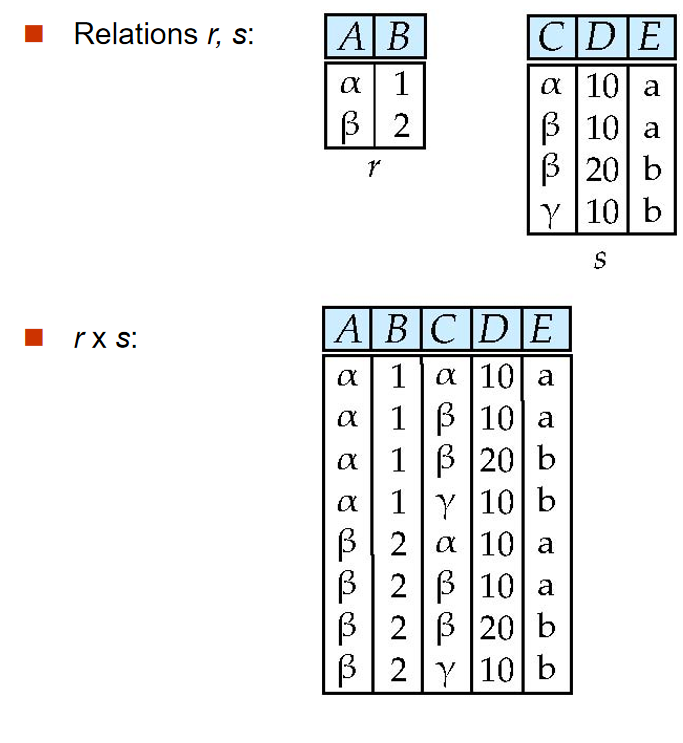
Cartesian Product:\(\times\)¶
笛卡尔积操作,返回两个关系的笛卡尔积。
例如,要找到所有教授和他们的课程,可以这样写:
\(\sigma_{instructor.ID=teaches.ID}(instructor \times teaches)\)
注意,两个关系要笛卡尔乘积,需要它们的属性不同。如果有相同的属性名,那么需要用rename操作。
Rename:\(\rho\)¶
重命名操作,重命名关系或属性。
假设有一个名为 instructor 的关系,包含属性 ID 和 name。
-
重命名关系:
将
instructor关系重命名为professor:\[ \rho_{professor}(instructor) \] -
重命名属性:
将
instructor关系中的ID属性重命名为instructor_id:\[ \rho_{instructor_{id}, name}(instructor) \] -
同时重命名关系和属性:
将
instructor关系重命名为professor,并将ID属性重命名为instructor_id:\[ \rho_{professor(instructor_{id}, name)}(instructor) \]
Example¶
🌰
Find the names of all instructors in the Physics department, along with the course_id of all courses they have taught
\(\Pi_{instructor.name,course\text{_}id}(\sigma_{dept\text{_}name="Physics"}(\sigma_{instructor.id=teaches.id}(instructor \times teaches)))\)
Additional Operations¶
Intersection:\(\cap\)¶
交操作,返回两个关系的交集。使用公式:
Natural Join:\(\bowtie\)¶
自然连接操作,返回两个关系的连接。自然连接是一种特殊的笛卡尔积,它只返回那些在连接属性(\(R \cap S\))上相等的元组。自然连接满足结合律和交换律。
Theta Jion¶
在自然连接的基础上加上一个条件。
写作:
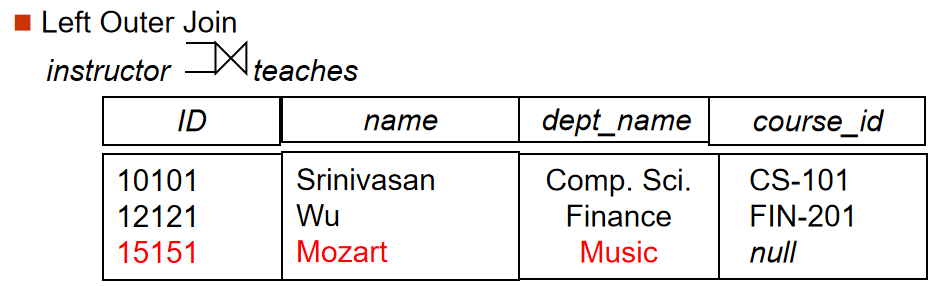
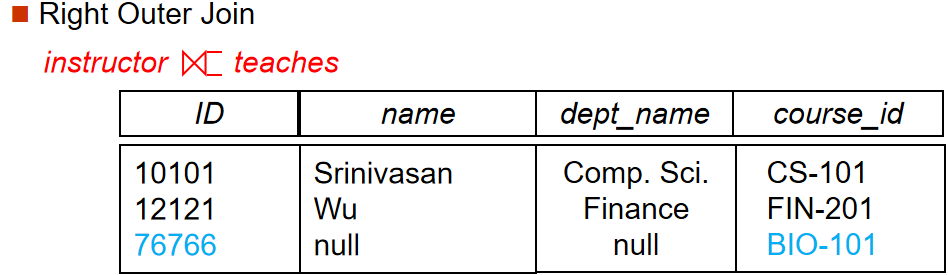
Outer Join: 外连接操作¶
返回两个关系的连接,同时返回那些在连接属性上不相等的元组。不存在的值用NULL填充。
对于下图的数据表:
-
Left Outer Join: 返回左关系的所有元组,同时返回那些在连接属性上相等的右关系的元组。
-
Right Outer Join: 返回右关系的所有元组,同时返回那些在连接属性上相等的左关系的元组。
-
Full Outer Join: 返回两个关系的所有元组,同时返回那些在连接属性上相等的元组。
半连接操作¶
半连接会从关系 r 中选择那些与关系 s 中至少一个元组满足连接条件\(\theta\)的元组。通俗的说,半连接是一种存在性测试,它检查关系 r 中的元组在关系 s 中是否存在满足特定条件的匹配项。
对于命令:select name from instructor where exists (select * from teaches where instructor.ID = teaches.ID and teaches.year = 2022)
-
选择出 teaches 表中 year 为 2022 的元组。
-
选择出 instructor 表中 ID 与 teaches 表中 ID 相等的元组。
-
选择出 instructor 表中 name 属性。
就可以写为如下的半连接:
NULL Values¶
与Null的比较会得到一个新的布尔值:Unknown。
-
Or: True or Unknown = True, False or Unknown = Unknown, Unknown or Unknown = Unknown.
-
And: True and Unknown = Unknown, False and Unknown = False, Unknown and Unknown = Unknown.
-
Not: Not Unknown = Unknown.
Assignment: \(\leftarrow\)¶
赋值操作,将一个关系赋值给一个变量。
例如:
这个操作将选择出dept_name为Finance的元组,并将其赋值给变量R。
Division: \(\div\)¶
除法操作,返回两个关系的商。
商的定义
给定关系 r(R) 和 s(S),其中 S 是 R 的子集,r \(\div\) s 是满足以下条件的最大关系 t(R-S):
简单来说,关系 r 除以关系 s 的结果是一个关系 t,t 包含 r 中所有与 s 中的元组组合后仍然在 r 中的元组。
除法可以使用如下的公式表示:
解释:
-
temp1: 首先,我们通过投影操作 \(\Pi_{R-S}(r)\),从关系
r中选择所有不在关系s中的属性(R-S),并将结果存储在temp1中。这相当于找到所有可能出现在结果关系t中的元组。 -
temp2: 接下来,我们计算
temp2。- \((temp1 \times s)\): 我们计算
temp1和s的笛卡尔积。这将temp1中的每个元组与s中的每个元组组合在一起。 - \(\Pi_{R-S,S}(r)\): 我们从关系
r中投影出属性 R-S 和 S,也就是关系 r 的所有属性。 - \((temp1 \times s) - \Pi_{R-S,S}(r)\): 我们从 \(temp1 \times s\) 中减去 \(\Pi_{R-S,S}(r)\)。这将删除所有在
r中存在的temp1和s的组合。剩下的元组就是那些与s组合后不在r中的temp1元组。 - \(\Pi_{R-S}((temp1 \times s) - \Pi_{R-S,S}(r))\): 我们从结果中投影出属性\(R-S\)。这将删除所有与
s组合后不在r中的temp1元组。
- \((temp1 \times s)\): 我们计算
-
result: 最后,我们计算
temp1 - temp2。这将从temp1中删除所有与s组合后不在r中的元组。剩下的元组就是关系r除以关系s的结果。
Extended Operations¶
Generalized Projection¶
在投影操作中允许使用表达式。
例如:
\(\Pi_{name, salary*1.1}(instructor)\)
Aggregation¶
聚合操作用于对关系中的元组进行汇总计算。它可以分为两种情况:
-
没有分组的聚合:
当没有指定分组属性时,聚合函数将应用于关系中的所有元组,计算出一个单一的结果。
表示形式:
\[ \gamma_{agg\_func(attribute)}(relation) \]例如,计算所有教师的平均工资:
\[ \gamma_{AVG(salary)}(instructor) \] -
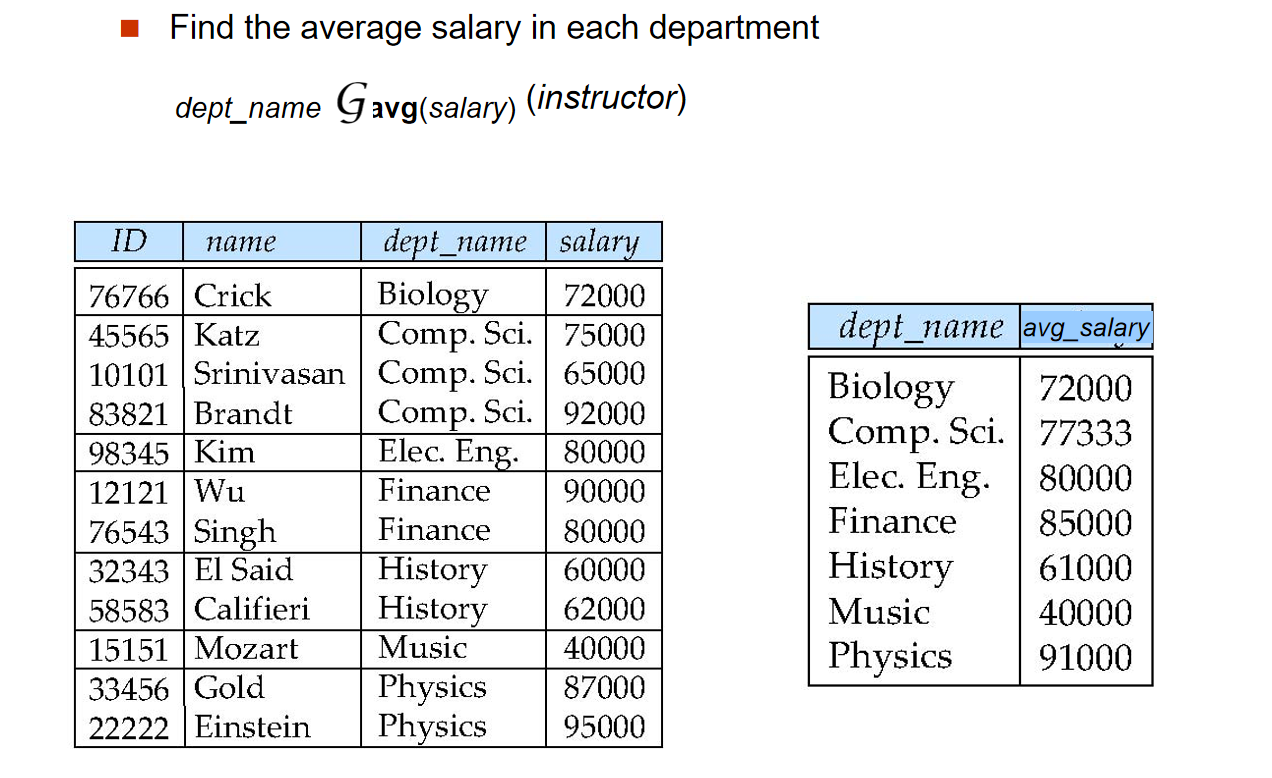
有分组的聚合:
当指定了分组属性时,关系将首先按照这些属性进行分组,然后聚合函数将分别应用于每个组中的元组,计算出每个组的结果。
表示形式:
\[ \sideset{_{grouping\_attribute_1, \dots, grouping\_attribute_n}}{} \gamma_{agg\_func(attribute)} (relation) \]例如,按照部门计算教师的平均工资:
\[ \sideset{_{dept\_name}}{AVG(salary)}\gamma (instructor) \]
在这个例子中,dept_name 是分组属性,AVG(salary) 是聚合函数。结果将包含每个部门的名称以及该部门教师的平均工资。