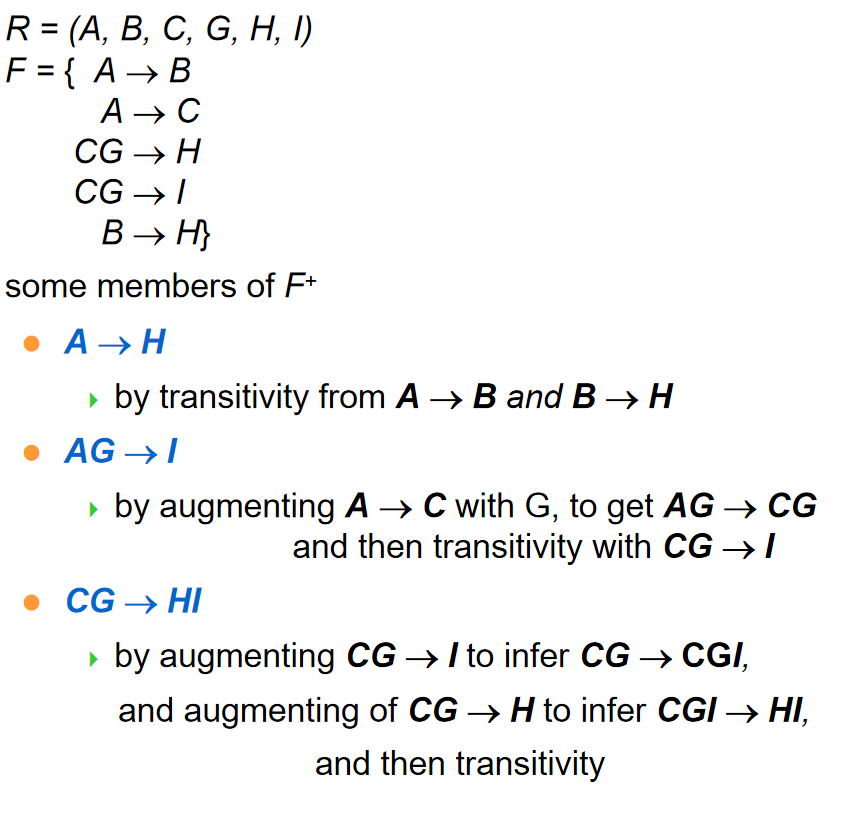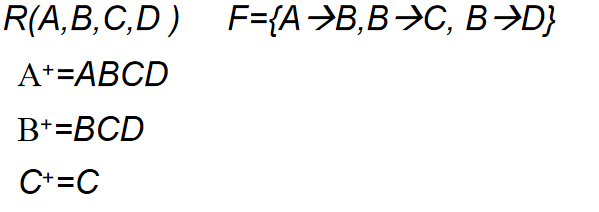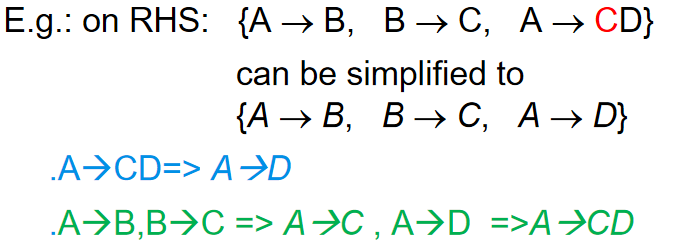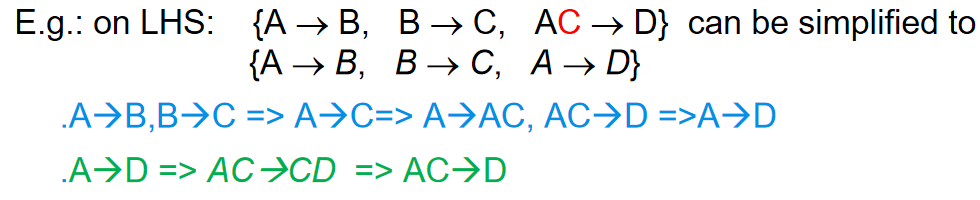关系数据库设计¶
约 3403 个字 25 张图片 预计阅读时间 17 分钟
介绍¶
引入
假设我们现在有如下关系模型:
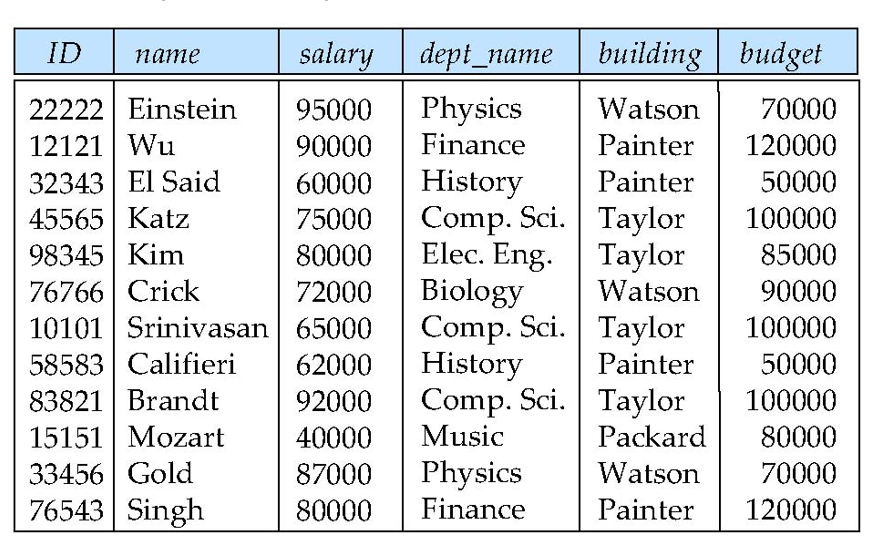
如果我们把instructor和department两个表合并,会怎么样?
这样的一个表会有什么问题,让我们把它称为一个"bad" relation?
-
Information repetition (信息重复):
instructor表中有很多dept_name属性的值是相同的,导致信息重复存储。
-
Insertion anomalies (插入异常):
- 如果我们想要插入一个新的系
dept_name,但是没有任何教授属于这个系,那么我们就无法插入这个系的信息。
- 如果我们想要插入一个新的系
-
Update difficulty (更新困难)
- 如果我们想要更新一个教授的系
dept_name,我们需要在多个地方进行更新,包括budget和building属性。
- 如果我们想要更新一个教授的系
那么,是什么原因导致这个表变成了一个"bad" relation呢?
我们可以发现,在关系模型中,属性之间存在依赖关系,正如我们之前所说的主键.只要知道了主键,就可以唯一确定一个元组.
在新的合成的表中,主键是ID.然而,department也能决定其他一些属性:budget和building.但在这里,department并不是一个candidate key,因为它无法唯一确定一个元组,因此我们应该把这个表分解成两个表.
所以,我们也可以定义什么是好的关系模型:
好的关系模型:
-
只有candidate key才能决定其他属性
-
也就是说,如果一个属性决定了其他属性,那么它必须是一个candidate key.
看完了合成,我们来看看表的分解.
我们把分解分成两种:
-
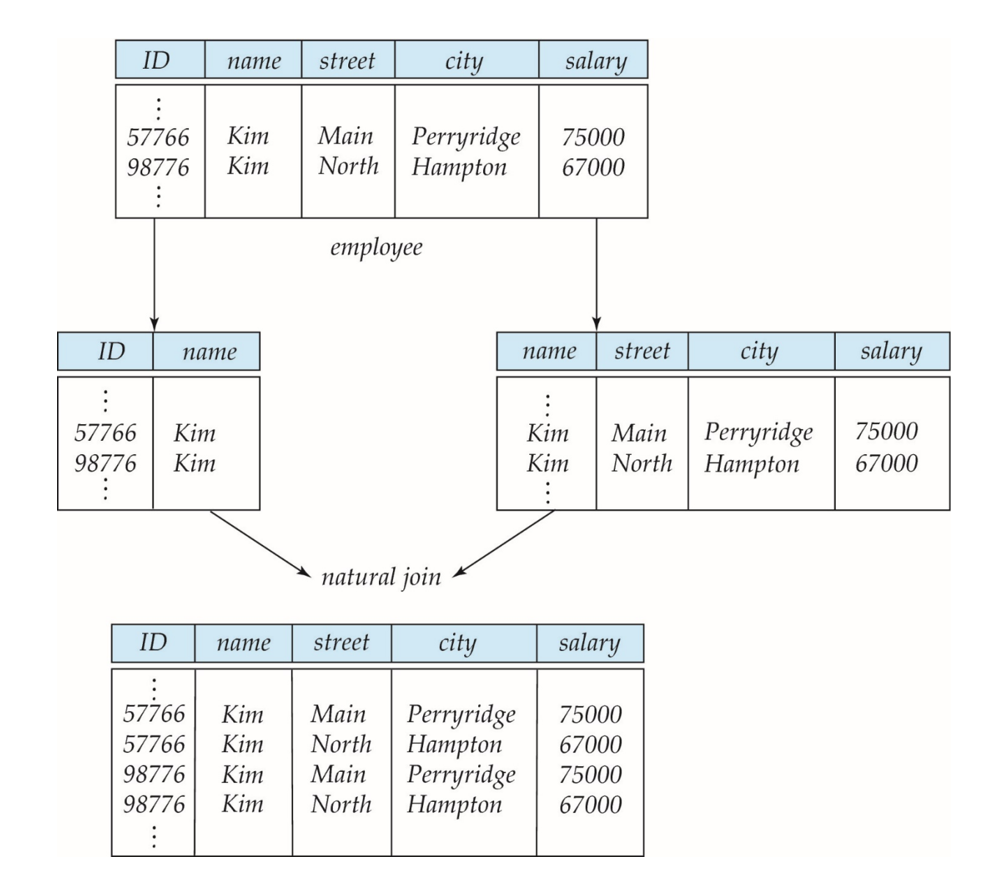
Lossy decomposition: 有损分解.分解后,我们无法从分解后的表中恢复原来的表.
-
定义:分解后无法通过连接操作完全恢复原始表
-
特点:
-
信息丢失
-
可能产生虚假元组
-
更多的元组意味着更多不确定性,即信息丢失
-
-
示例:
- 主键选择不当(如图中错误地使用"名字"作为主键)
-
-
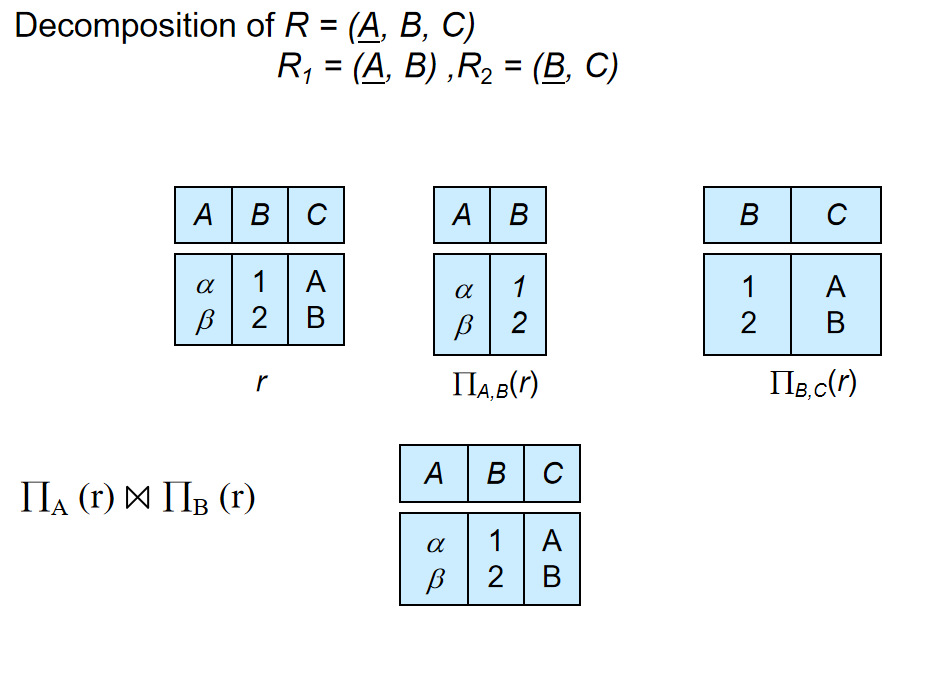
Lossless decomposition: 无损分解.分解后,我们可以从分解后的表中恢复原来的表.
-
无损条件: $$ \pi_{R_1}(r) \bowtie \pi_{R_2}(r) = r $$
-
判断标准(至少满足其一):
-
$ R_1 \cap R_2 \rightarrow R_1 $
-
$ R_1 \cap R_2 \rightarrow R_2 $
-
即公共属性是一个表的超键
-
-
First Normal Form¶
-
定义:关系模式R处于第一范式,当且仅当R的所有属性的域都是原子的。
-
原子域:域是原子的,如果其元素被视为不可分割的单元。
-
非原子域的例子:
-
姓名集合、复合属性
-
可以被分解成多个部分的标识号,如CS101->CS和101
-
-
关于原子性的说明:
-
原子性实际上是域元素使用方式的一种属性
-
例如:字符串通常被视为不可分割的
-
假设学生被赋予形如CS0012或EE1127的学号
-
如果提取前两个字符来确定院系,则学号的域就不是原子的
-
这样做是一个不好的设计:导致信息被编码在应用程序中,而不是在数据库中
-
-
Devise a Theory for the Following¶
如果一个关系R不是一个好的关系,那么我们作如下操作
-
将R分解为\({R_1, R_2, \ldots, R_n}\)
-
使得每个\(R_i\)都是一个好的关系
Normal Forms(NF):
1NF -> 2NF -> 3NF -> BCNF -> 4NF
Functional Dependencies¶
让R是一个关系范式,并且对于属性\(alpha\)和\(beta\):
那么我们称函数依赖 $$ \alpha \rightarrow \beta $$
保持在R上,当且仅当对于任何合法关系r(R),其任意元组\(t_1\),\(t_2\)满足:
-
K是关系范式R的超键当且仅当\(K\rightarrow R\)
-
K是关系范式R的主键当且仅当K是超键,并且没有任何真子集K'是超键.用数学语言表示就是:
\[ K \text{ is a superkey} \iff K \rightarrow R \text{ and } K' \nrightarrow R \text{ for all } K' \subset K \]
A functional dependency is trivial if it is satisfied by all relations
比如:
-
name -> name
-
{ID,name}->ID
一般的,如果\(\beta \subseteq \alpha\),那么\(\alpha \rightarrow \beta\)是平凡的
Closure(闭包)¶
Closure of a Set of Functional Dependencies¶
Given a set F of functional dependencies, there are certain other functional dependencies that are logically implied by F.
For example: If A -> B and B -> C, then we can infer that A -> C
我们定义:The set of all functional dependencies logically implied by F is the closure of F.
也即,闭包是一个包含所有函数依赖的集合,也就是F的所有函数依赖的集合.我们用\(F^+\)表示.
Example
F={A->B, B->C}
\(F^+ = {A->B, B->C, A->C,AB->B,AB->C,\ldots}\)
我们可以使用阿姆斯特朗定律来找到闭包
Definition
-
如果 \(\beta \subseteq \alpha\),那么 \(\alpha \rightarrow \beta\) (自反律 reflexivity)
-
如果 \(\alpha \rightarrow \beta\),那么 \(\alpha\gamma \rightarrow \beta\gamma\) (增补律 augmentation)
-
如果 \(\alpha \rightarrow \beta\) 且 \(\beta \rightarrow \gamma\),那么 \(\alpha \rightarrow \gamma\) (传递律 transitivity)
这三条定律是:
-
Sound(正确有效的) (generate only functional dependencies that actually hold)
-
Complete(完备的) (generate all functional dependencies that hold).
我们从这三条定律中也推出了另外三条additional rules:
-
如果 \(\alpha \rightarrow \beta\) 且 \(\alpha \rightarrow \gamma\),那么 \(\alpha \rightarrow \beta\gamma\) (合并 union)
-
如果 \(\alpha \rightarrow \beta\gamma\),那么 \(\alpha \rightarrow \beta\) 且 \(\alpha \rightarrow \gamma\) (分解 decomposition)
-
如果 \(\alpha \rightarrow \beta\) 且 \(\beta\gamma \rightarrow \delta\),那么 \(\alpha\gamma \rightarrow \delta\) (伪传递 pseudotransitivity)
Closure of Attribute Sets¶
Given a set of attributes X, the closure of X with respect to a set of functional dependencies F is the set of attributes that are functionally determined by X under F.
也就是看看X能决定哪些属性.
The closure of X is denoted by \(X^+\).
Uses of Attribute Closure¶
属性闭包算法有以下几个用途:
-
测试超键:
- 要测试 \(\alpha\) 是否是超键,我们计算 \(\alpha^+\),然后检查 \(\alpha^+\) 是否包含 \(R\) 的所有属性。
-
测试函数依赖:
-
要检查函数依赖 \(\alpha \rightarrow \beta\) 是否成立(换句话说,是否在 \(F^+\) 中),只需检查 \(\beta\) 是否包含于 \(\alpha^+\)。
-
即我们使用属性闭包计算 \(\alpha^+\),然后检查它是否包含 \(\beta\)。
-
-
计算 \(F\) 的闭包:
- 对于每个 \(\alpha \subseteq R\),我们找到闭包 \(\alpha^+\),然后对于每个 \(S \subseteq \alpha^+\),我们输出一个函数依赖 \(\alpha \rightarrow S\)。
Canonical Cover(正则覆盖)¶
函数依赖集可能会有冗余,包括:
-
冗余的函数依赖:
- 例如:在 \(A \rightarrow B\) ,\(A \rightarrow C\)和 \(B \rightarrow C\),中,\(A \rightarrow C\)是冗余的,因为它可以从 \(A \rightarrow B\)和 \(B \rightarrow C\)中推导出来。
-
冗余的属性
-
LHS:
-
RHS:
-
因此,我们定义一个函数依赖集的正则覆盖是一个最小的函数依赖集,它与原来的函数依赖集等价.
无关属性 (Extraneous Attributes)
考虑函数依赖集F和其中的某个函数依赖 \(\alpha \rightarrow \beta\),无关属性有两种类型:
-
左侧的无关属性
如果属性A在\(\alpha\)中是无关的,意味着:
-
\(A \in \alpha\)
-
F逻辑上包含\((α-A) \rightarrow \beta\)
通俗理解:即使移除A,其余属性仍然能决定\(\beta\)
例子: 在F = {\(A \rightarrow C\), \(AB \rightarrow C\)}中,B在"\(AB \rightarrow C\)"的左侧是无关的,因为单靠A就能决定C。
-
-
右侧的无关属性
如果属性A在\(\beta\)中是无关的,意味着:
-
\(A \in \beta\)
-
F-{\(\alpha \rightarrow \beta\)}∪{\(\alpha \rightarrow (\beta-A)\)}逻辑上包含\(\alpha \rightarrow A\)
通俗理解:从其他依赖也能推导出\(\alpha \rightarrow A\)
例子: 在F = {\(A \rightarrow C\), \(AB \rightarrow CD\)}中,C在"\(AB \rightarrow CD\)"的右侧是无关的,因为我们已经知道\(A \rightarrow C\),所以在\(AB \rightarrow CD\)中再包含C是多余的。
-
上述情况的反向推导是显然成立的,因为一个更强的函数依赖集可以推导出一个更弱的函数依赖集.
OK,现在我们来给出正则覆盖完整的定义:
正则覆盖 (Canonical Cover)
函数依赖集F的正则覆盖是一个函数依赖集\(F_c\),满足:
-
F逻辑上包含\(F_c\)中的所有依赖
-
\(F_c\)逻辑上包含F中的所有依赖
-
\(F_c\)中没有任何函数依赖包含无关属性
-
\(F_c\)中每个函数依赖的左侧都是唯一的
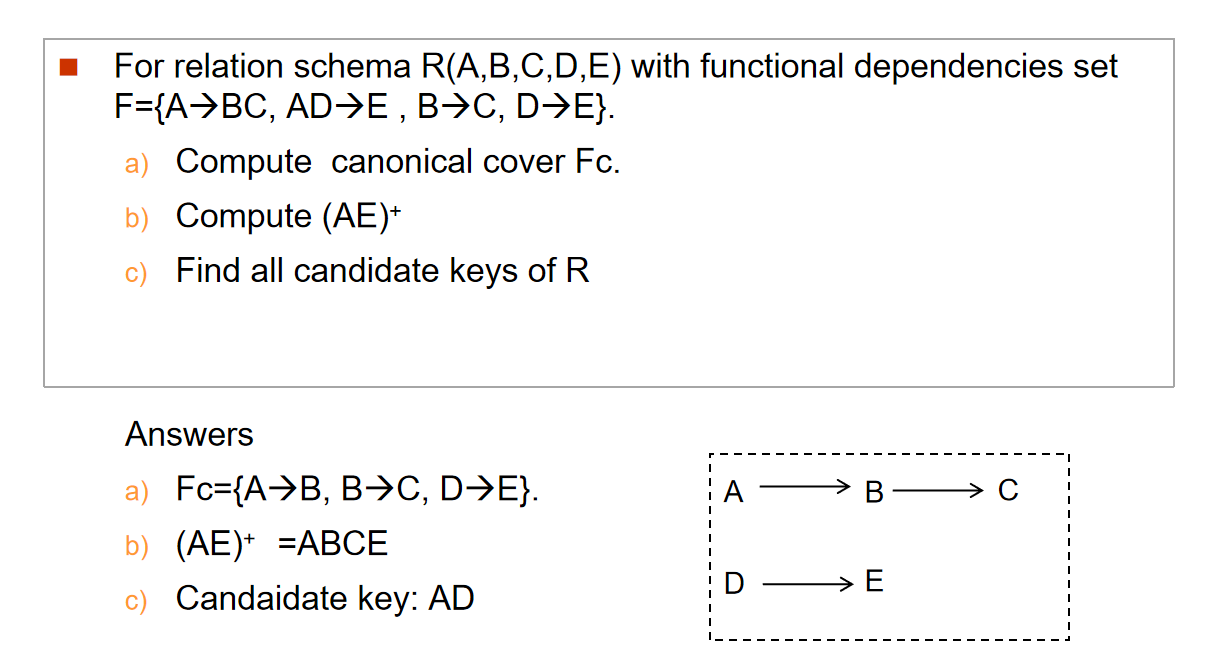
正则覆盖的计算¶
我们用如下方法计算正则覆盖:
Boyce-Codd Normal Form(BCNF)¶
一个关系范式R在一个函数集合F下处于BCNF,要求对于所有\(F^+\)的函数依赖\(\alpha \rightarrow \beta\),至少满足如下的一个条件:
-
\(\alpha \rightarrow \beta\) 是平凡的(即\(\beta \subseteq \alpha\))
-
\(\alpha\)是R的超键
Decomposing a Schema into BCNF¶
假设我们有一个关系模式 $ R $,并且存在一个非平凡依赖 $ \alpha \rightarrow \beta $,它导致违反了 BCNF(Boyce-Codd范式)。
我们将 $ R $ 分解为以下两个子关系:
- $ \alpha \cup \beta $
- $ R - (\beta - \alpha) $
在我们上面的例子中:
-
\(\alpha = \text{dept_name}\)
-
$ \beta = { \text{building}, \text{budget} } $
因此,关系 inst_dept 被替换为:
-
\(\alpha \cup \beta = \{ \text{dept_name}, \text{building}, \text{budget} \}\)
-
\(R - (\beta - \alpha) = \{ \text{ID}, \text{name}, \text{salary}, \text{dept_name} \}\)
直白地讲,就是把不满足的函数依赖里的属性分解到一个新的表中,并且把原来的表中去掉这些属性。还要选出一个属性作为公共属性与新的表的主键,在这里就是dept_name。
BCNF and Dependency Preservation¶
Dependency Preservation
-
如果通过检验单一关系上的函数依赖,就能确保所有的函数依赖成立, 那么这样的分解是依赖保持的
-
或者,原来关系R上的每一个函数依赖,都可以在分解后的单一关系上得到检验或者推导得到。
设 $ F_i $ 是 $ F^+ $ 中所有只包含 $ R_i $ 中属性的函数依赖的集合。
即$ F_i $ 是将 $ F $ 限制在子关系 $ R_i $ 上的结果(称为对 $ R_i $ 的限制 restriction)。
一个分解是依赖保持的(Dependency Preserving),当且仅当:
Because it is not always possible to achieve both BCNF and dependency preservation, we consider a weaker normal form, known as third normal form.
Third Normal Form¶
正如上面所说,BCNF是一个很强的范式,但是它并不总是能保持函数依赖.
因此,我们定义一个更弱的范式,称为第三范式(3NF),它的特点是:
-
允许一些冗余
-
总是依赖保持的
-
总可以将任意关系模式分解为满足3NF的子关系,且分解是无损连接、依赖保持的
Third Normal Form (3NF)
一个关系模式 \( R \) 属于第三范式(3NF),当对于所有在 \( F^+ \) 中的函数依赖 \( \alpha \rightarrow \beta \),满足以下至少一个条件:
-
\( \alpha \rightarrow \beta \) 是平凡依赖(即 \( \beta \subseteq \alpha \))
-
\( \alpha \) 是 \( R \) 的一个超键(superkey)
-
对于 \( \beta - \alpha \) 中的每一个属性 \( A \),都有:
-
If a relation is in BCNF it is in 3NF (since in BCNF one of the first two conditions above must hold).
-
Third condition is a minimal relaxation of BCNF to ensure dependency preservation.
3NF分解算法如下图:
-
令 \( F_c \) 是函数依赖集 \( F \) 的标准覆盖(Canonical Cover)。
-
初始化计数器:\( i := 0 \)
-
对于 \( F_c \) 中的每一个函数依赖 \( \alpha \rightarrow \beta \),执行:
- \( i := i + 1 \)
-
创建关系模式:\( R_i := \alpha \cup \beta \)
-
这一步确保了依赖保持
-
如果当前构造出的所有子关系 \( R_j \)(\( 1 \leq j \leq i \))都不包含 \( R \) 的候选键,则:
- \( i := i + 1 \)
-
任选一个 \( R \) 的候选键 \( K \),令 \( R_i := K \)
-
这一步确保了无损连接
-
【可选步骤:删除冗余关系模式】
- 重复以下操作,直到没有可以删除的关系模式:
- 如果某个关系 \( R_j \) 完全包含在另一个关系 \( R_k \) 中,则:
- 删除 \( R_j \),即设 \( R_j := R_i \),并令 \( i := i - 1 \)
- 重复以下操作,直到没有可以删除的关系模式:
-
最终返回子关系集合:
\( (R_1, R_2, \ldots, R_i) \)
规范化的目标¶
假设R是一个关系模式,F是其上的函数依赖集。我们需要:
-
判断关系模式R是否处于“好”范式。
-
如果关系模式R不处于“好”范式,则将其分解为一组关系模式 \(\{R_1, R_2, ..., R_n\}\),使得:
-
每个分解后的关系模式 \(R_i\) 都处于好范式(例如,BCNF或3NF)。
-
该分解是无损连接的。
-
最好,该分解还应保持函数依赖。
-
ER模型与NF模型的关系¶
Multivalued Dependencies(多值依赖)¶
设R是一个关系模式,\(\alpha \subseteq R\)且\(\beta \subseteq R\)。多值依赖\(\alpha \twoheadrightarrow \beta\)
在R上成立的条件是:对于任何合法关系r(R)中的任意两个元组t1和t2,如果t1[\(\alpha\)] = t2[\(\alpha\)],那么在r中必然存在元组t3和t4,使得:
- t3[\(\alpha\)] = t4[\(\alpha\)] = t1[\(\alpha\)] = t2[\(\alpha\)](这四个元组在\(\alpha\)上的值相同)
- t3[\(\beta\)] = t1[\(\beta\)](t3在\(\beta\)上的值与t1相同)
- t3[R - \(\alpha\) - \(\beta\)] = t2[R - \(\alpha\) - \(\beta\)](t3在剩余属性上的值与t2相同)
- t4[\(\beta\)] = t2[\(\beta\)](t4在\(\beta\)上的值与t2相同)
- t4[R - \(\alpha\) - \(\beta\)] = t1[R - \(\alpha\) - \(\beta\)](t4在剩余属性上的值与t1相同)
看上去很晦涩,我们来看看例子:
通俗来讲,多值依赖就是一个属性决定了另一个属性的集合,而且与剩下的属性可以随意组合.
Theory of MVDs
- 如果\(\alpha \rightarrow \beta\),那么\(\alpha \twoheadrightarrow \beta\)
后面不想写了,看这里