浙江大学2018-19春夏《高级数据结构与算法分析》期中模拟练习-陈越

开始时间2016/01/01 08:00:00

结束时间2038/01/18 08:00:00

答题时长45分钟

考生

得分97

总分100

判断题得分：32总分：35

R1-1

When measuring the relevancy of the answer set, if the precision is low but the recall is high, it means that most of the relevant documents are missing, but most of the retrieved documents are relevant.

(4分)

R1-2

A perfectly balanced tree forms if keys 1 to $2^k -1$ are inserted in order into an initally empty leftist heap.

(4分)

R1-3

In a red-black tree, the number of rotations in the DELETE operation is O(1).

(3分)

R1-4

For the recurrence equation $T(N)=aT(N/b)+f(N)$ , if $af(N/b)=f(N)$ , then $T(N)=\Theta (N log_b N)$ .

(4分)

R1-5

Making $N$ insertions into an initally empty binomial queue takes $O(N)$ time in the worst case.

(3分)

R1-6

In amortized analysis, a good potential function should always assume its maximum at the start of the sequence.

(3分)

R1-7

Finding the minimum key from a splay tree will result in a tree with its root having no left subtree.

(4分)

R1-8

In an AVL tree, it is possible to have this situation that the balance factors of a node and both of its children are all -1.

(4分)

R1-9

In backtracking, if different solution spaces have different sizes, start testing from the partial solution with the smallest space size would have a better chance to reduce the time cost.

(3分)

R1-10

The time bound of the FIND operation in a B+ tree containing $N$ numbers is $O(\log N)$ , no matter what the degree of the tree is.

(3分)

单选题得分：40总分：40

R2-1

Given the following game tree, which node in the right subtree is the first node to be pruned with α-β pruning algorithm?

(5分)

R2-2

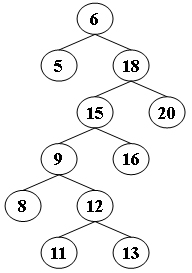
Insert { 5, 1, 7, 8, 21, 2, 12, 19, 13, 0 } into an initially empty 2-3 tree (with splitting). Which one of the following statements is FALSE?

(5分)

13 and 19 are in the same node

the first key stored in the root is 12

the parent of the node containing 8 has 3 children

there are 5 leaf nodes

R2-3

There are 8000 documents in the database. The statistic data for one query are shown in the following table. The precision is: __

	Relevant	Irrelevant
Retrieved	1000	1000
Not Retrieved	2000	4000

(5分)

50%

33%

12.5%

20%

R2-4

For the result of accessing 11 in the splay tree in the following figure, besides saying that 11 must be the root, which one of the following statements is also TRUE?

(5分)

6 and 18 are siblings

12 is a leaf node

9 and 18 are siblings

12 and 18 are siblings

R2-5

A queue can be implemented by using two stacks $S_A$ and $S_B$ as follows:

To enqueue $x$ , we push $x$ onto $S_A$ .
To dequeue from the queue, we pop and return the top item from $S_B$ . However, if $S_B$ is empty, we first fill it (and empty $S_A$ ) by popping the top item from $S_A$ , pushing this item onto $S_B$ , and repeat until $S_A$ is empty.

Assuming that push and pop operations take $O(1)$ worst-case time, please select a potential function $\phi$ which can help us prove that enqueue and dequeue operations take $O(1)$ amortized time (when starting from an empty queue).

(5分)

$\phi = 2|S_A|$

$\phi = |S_B|$

$\phi = 2|S_B|$

$\phi = |S_A|$

R2-6

3-way-mergesort : Suppose instead of dividing in two halves at each step of the mergesort, we divide into three one thirds, sort each part, and finally combine all of them using a three-way-merge. What is the overall time complexity of this algorithm ?

(5分)

$O(n)$

$O(n\log n)$

$O(n^2 \log n)$

$O(n(\log^2 n))$

R2-7

Delete a node $v$ from an AVL tree $T_1$ , we can obtain another AVL tree $T_2$ . Then insert $v$ into $T_2$ , we can obtain another AVL tree $T_3$ . Which one(s) of the following statements about $T_1$ and $T_3$ is(are) true?

I、If $v$ is a leaf node in $T_1$ , then $T_1$ and $T_3$ might be different.
II、If $v$ is not a leaf node in $T_1$ , then $T_1$ and $T_3$ must be different.
III、If $v$ is not a leaf node in $T_1$ , then $T_1$ and $T_3$ must be the same.

(5分)

II only

I and II only

I and III only

I only

R2-8

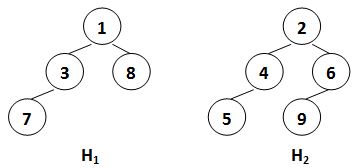
Merge the two leftist heaps in the following figure. Which one of the following statements is FALSE?

(5分)

6 is the left child of 2

the null path length of 6 is the same as that of 2

1 is the root with 3 being its right child

Along the left most path from top down, we have 1, 2, 4, and 5

程序填空题得分：25总分：25

R5-1

The functions BinQueue_Find and Recur_Find are to find X in a binomial queue H. Return the node pointer if found, otherwise return NULL.

BinTree BinQueue_Find( BinQueue H, ElementType X )
{
    BinTree T, result = NULL;
    int i, j; 

    for( i=0, j=1; j<=H->CurrentSize; i++, j*=2) {  /* for each tree in H */
        T= H->TheTrees[i];
        if ( X (5分) ){  /* if need to search inside this tree */
            result = Recur_Find(T, X);
            if ( result != NULL ) return result;
        } 
    }
    return result;
}

BinTree Recur_Find( BinTree T, ElementType X )
{
    BinTree result = NULL;
    if ( X==T->Element ) return T;
    if ( (5分) ){
        result = Recur_Find(T->LeftChild, X);
        if ( result!=NULL ) return result;
    } 
    if ( T->NextSibling!=NULL )
        result = Recur_Find(T->NextSibling, X);
    return result;
}

R5-2

The functions IsRBT is to check if a given binary search tree T is a red-black tree. Return true if T is, or false if not.

The red-black tree structure is defined as the following:

typedef enum { red, black } colors;
typedef struct RBNode *PtrToRBNode;
struct RBNode{
    int Data;
    PtrToRBNode Left, Right, Parent;
    int BlackHeight;
    colors Color;
};
typedef PtrToRBNode RBTree;

Please fill in the blanks.

bool IsRBT( RBTree T )
{
    int LeftBH, RightBH;
    if ( !T ) return true;
    if ( T->Color == black ) T->BlackHeight = 1;
    else {
         if ( T->Left && (5分)) return false;
         if ( T->Right && (T->Right->Color == red) ) return false;
    }
    if ( !T->Left && !T->Right ) return true;
    if ( (5分)) {
       if ( T->Left ) LeftBH = T->Left->BlackHeight;
       else LeftBH = 0;
       if ( T->Right ) RightBH = T->Right->BlackHeight;
       else RightBH = 0;
       if ( LeftBH == RightBH ) { 
          (5分);
          return true;
       }
       else return false;
    }
    else return false;
}